题目内容
2．
如图，已知AB⊥CD垂足为O，EF经过点O．如果∠1=30°，则∠2等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 直接利用垂线的定义得出∠AOD=90°，进而利用对顶角定义得出∠FOD=30°，即可得出∠2的度数．
解答 解：∵AB⊥CD垂足为O，
∴∠AOD=90°，
∵∠1=30°，
∴∠FOD=30°，
∴∠2=90°-30°=60°．
故选：C．
点评 此题主要考查了垂线定义以及对顶角的定义，得出∠FOD的度数是解题关键．
练习册系列答案
相关题目
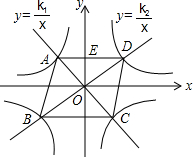如图，经过O的直线AC，BD分别与反比例函数y=$\frac{{k}_{1}}{x}$（k1＜0），y=$\frac{{k}_{2}}{x}$（k＞0）相交于点A，C，B，D，且AC⊥BD
如图，在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3）．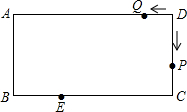
如图，在矩形ABCD中，AB=5cm，BC=10cm．动点P从点D出发，沿折线D-C-B-A-D以2cm/s的速度运动，动点Q从点D出发．沿D-A-B-C-D以1cm/s的速度运动．若动点P、Q同时出发，相遇是停止运动．设运动时间为ts．点E为BC边上一点，且BE=3cm．
如图，在四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点，且EG、FH交于点O．
如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B 300m，结果他在水中实际游了500m，求该河流的宽度为400m．