题目内容
14.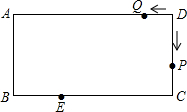 如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.
如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.(1)求P、Q从出发到相遇所用的时间;
(2)在P、Q的运动过程中,下列命题能否成立?如果能,分别求出相应t的值;如果不能,请说明理由:
①线段PQ经过矩形ABCD的对称中心.
②以A、E、P、Q为顶点的四边形是平行四边形.
分析 (1)由题意得出方程t+2t=2(5+10),解方程即可解得t=10;
(2)①由矩形ABCD的中心对称性得出AQ=CP,即10-t=2t-5,解方程即可;
②由①得:P、Q在点A处相遇,由平行四边形的判定和题意得出点P应在BC上,分两种情况:
(A)当点P在点E的右侧时,得出AQ=EP,得出方程,解方程即可;
(B)当点P在点E的左侧时,得出AQ=PE,得出方程,解方程即可.
解答 解:(1)由题意得:t+2t=2(5+10),
解得:t=10,
∴P、Q从出发到相遇所用的时间为10s;
(2)①成立;理由如下:
∵矩形ABCD是中心对称图形,
若线段PQ经过对称中心O,则AQ=CP,
即10-t=2t-5,
解得:t=5,
∴当t=5s时,线段PQ经过矩形ABCD的对称中心;
②成立:理由如下:
由①得:P、Q在点A处相遇,
∵AD∥BC,
∴以A、E、P、Q为顶点的四边形是平行四边形,
则点P应在AB或BC或CD上,Q在AD上,
而点P在AB或CD上时均不能构成平行四边形,
∴点P应在BC上,分两种情况:
(A)当点P在点E的右侧时,为平行四边形AEPQ,
此时应有AQ=EP,
即10-t=(10-3)+5-2t,
解得:t=2,
∵点P应在BC上,
∴t>$\frac{5}{2}$,
∴t=2<$\frac{5}{2}$,不合题意,舍去;
(B)当点P在点E的左侧时,为平行四边形APEQ,
此时应有AQ=PE,
即10-t=2t-(10-3)-5,
解得:t=$\frac{22}{3}$,
∵点P在点E的左侧,且点P应在BC上,
∴6<t<$\frac{15}{2}$,
而6<$\frac{22}{3}$<$\frac{15}{2}$,
∴t=$\frac{22}{3}$时,符合题意,
综上所述,当t=$\frac{22}{5}$s时,四边形APEQ为平行四边形.
点评 本题是四边形综合题目,考查了矩形的性质、平行四边形的判定、解方程等知识;本题综合性强,有一定难度,特别是(2)②需要进行分类讨论才能得出结果.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案 如图,已知AB⊥CD垂足为O,EF经过点O.如果∠1=30°,则∠2等于( )
如图,已知AB⊥CD垂足为O,EF经过点O.如果∠1=30°,则∠2等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
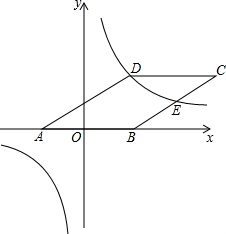 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式. 如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?
如图所示,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,你能求出CD的长吗?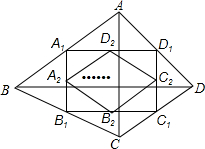 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( ) 如图,已知DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于点O.求证:BE=CD,∠ACD=∠AEB.
如图,已知DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于点O.求证:BE=CD,∠ACD=∠AEB.