题目内容
7. 如图在△ABC中,AB=AC,D是BC上任意一点(D不与B、C重合),H为AD中点,连CH并延长交AB于E
如图在△ABC中,AB=AC,D是BC上任意一点(D不与B、C重合),H为AD中点,连CH并延长交AB于E(1)当BD:DC=5:8时,求BE:EA;
(2)当AE与BE满足什么条件时,AD⊥BC,并加以证明;
(3)是否存在这样的D点,使E为AB的中点?若存在求出BD:DC,若不存在,请加以证明.
分析 (1)作DN∥CE交AB于N,根据平行线分线段成比例定理计算;
(2)根据等腰三角形的三线合一得到BD=DC,根据平行线分线段成比例定理计算;
(3)根据三角形中位线定理解答.
解答 解:(1)如图1,作DN∥CE交AB于N,
∴BE:EN=BD:DC=5:8,
∵DN∥CE,H为AD中点,
∴HE=EA,
∴BE:EA=5:16;
(2)当AE:BE=1:2时,AD⊥BC, 证明:作DF∥CE交AB于F,
证明:作DF∥CE交AB于F,
∵AB=AC,AD⊥BC,
∴BD=DC,
∵DF∥CE,BD=DC,H为AD中点,
∴BF=FE,FE=EA,
∴AE:BE=1:2时,AD⊥BC;
(3)不存在这样的D点,使E为AB的中点.
∵E为AB的中点,H为AD中点,
∴EC∥BC.
∴不存在这样的D点,使E为AB的中点.
点评 本题考查的是等腰三角形的性质、三角形中位线定理以及平行线分线段成比例定理的应用,掌握等腰三角形的三线合一、三角形中位线定理是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
18. 如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
 如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )
如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是( )| A. | $\frac{1}{2}$π | B. | $\frac{1}{2}π$+1 | C. | π | D. | π+1 |
2.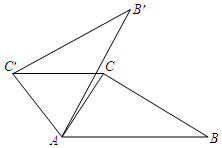 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
12.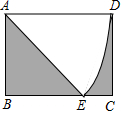 在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
 在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )
在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC于E,连接DE,则阴影部分的面积为( )| A. | $\frac{π}{4}$ | B. | 2$\sqrt{2}$-$\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | 2$\sqrt{2}$-$\frac{π}{2}$ |
19. 如图,在⊙O中,AC∥OB,∠BAC=25°,则∠ADB的度数为( )
如图,在⊙O中,AC∥OB,∠BAC=25°,则∠ADB的度数为( )
 如图,在⊙O中,AC∥OB,∠BAC=25°,则∠ADB的度数为( )
如图,在⊙O中,AC∥OB,∠BAC=25°,则∠ADB的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
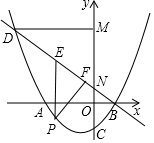 如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,-$\frac{5}{2}$).直线y=mx+$\frac{3}{2}$过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.