题目内容
2.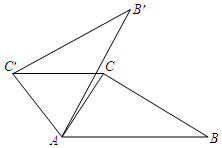 如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )
如图,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数至少为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
分析 据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.
解答 解:∵CC′∥AB,
∴∠ACC′=∠CAB=55°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°-2∠ACC′=180°-2×55°=70°,
∴∠CAC′=∠BAB′=70°.
故选C.
点评 本题考查了旋转的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
13.若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是$\frac{{\sqrt{2}}}{2}$的概率为( )
| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
10.用科学记数法方法表示0.0000201得( )
| A. | 0.201×10-4 | B. | 2.01×10-6 | C. | 20.1×10-6 | D. | 2.01×10-5 |
17.如图,∠1和∠2是对顶角的图形是( )
| A. |  | B. |  | C. |  | D. |  |
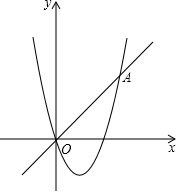 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点. 如图在△ABC中,AB=AC,D是BC上任意一点(D不与B、C重合),H为AD中点,连CH并延长交AB于E
如图在△ABC中,AB=AC,D是BC上任意一点(D不与B、C重合),H为AD中点,连CH并延长交AB于E 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC并延长,交切线BD于点D,连接OC.若∠BOC=100°,则∠D=40度.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC并延长,交切线BD于点D,连接OC.若∠BOC=100°,则∠D=40度.