Question

17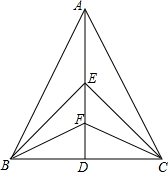．如图，在△ABC中，AB=AC，点E、F是中线AD上的两点，则图中可证明为全等的三角形有（　　）

• A． 3对
• B． 4对
• C． 5对
• D． 6对

Answer 1

分析 先根据等腰三角形的性质得出AD是线段BC的垂直平分线，AD是∠BAC的平分线，故可得出△ABD≌△ACD，同理可得出其余全等的三角形．

解答 解：∵在△ABC中，AB=AC，AD是BC的中线，
∴AD⊥BC，∠BAD=∠CAD．
在△ABD与△ACD中，
$\left\{\begin{array}{l}AB=AC\\∠BAD=∠CAD\\ BD=CD\end{array}\right.$，
∴△ABD≌△ACD（SAS）．
同理可得，△ABE≌△ACE，△ABF≌△ACF，△EBF≌△ECF，△EBD≌△ECD，△FBD≌△FCD，
∴图中可证明为全等的三角形有6对．
故选D．

点评 本题考查的是全等三角形的判定，熟知等腰三角形三线合一的性质及全等三角形的判定定理是解答此题的关键．