题目内容
8.解方程与不等式组:(1)$\frac{5}{x-2}$+1=$\frac{x-1}{2-x}$
(2)$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0}\\{3-4(x-1)<1}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:5+x-2=1-x,
解得:x=-1,
经检验x=-1是分式方程的解;
(2)$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0①}\\{3-4(x-1)<1②}\end{array}\right.$,
由①得:x≤2,
由②得:x>$\frac{3}{2}$,
则不等式组的解集为$\frac{3}{2}$<x≤2.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.次数为3的单项式可以是( )
| A. | 3ab | B. | ab2 | C. | a3+b3 | D. | a3b |
3.自2016年1月21日开建的印尼雅万高铁是中国和印尼合作的重大标志性项目,这条高铁的总长为152公里.其中“152公里”用科学记数法可以表示为( )
| A. | 0.152×106m | B. | 1.52×105m | C. | 1.52×106m | D. | 152×105m |
17.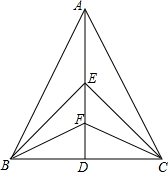 如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )
如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )
 如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )
如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
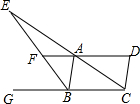 在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E.
在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E. 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.