题目内容
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|. 利用数形结合思想回答下列问题:

(1)数轴上表示1和5两点之间的距离是 ,数轴上表示2和-1的两点之间的距离是 ;
(2)数轴上表示x和-1的两点之间的距离表示为 ;
(3)若x表示一个有理数,且-4<x<2,则|x-2|-|x+4|= ;
(4)利用数轴求出|x+3|+|x+4|的最小值,并写出此时x可取哪些整数值?
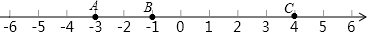

(1)数轴上表示1和5两点之间的距离是
(2)数轴上表示x和-1的两点之间的距离表示为
(3)若x表示一个有理数,且-4<x<2,则|x-2|-|x+4|=
(4)利用数轴求出|x+3|+|x+4|的最小值,并写出此时x可取哪些整数值?
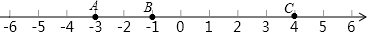
考点:数轴,绝对值
专题:
分析:(1)根据数轴上两点间的距离是大数减小数,可得答案;
(2)根据数轴上两点间的距离是大数减小数,可得答案;
(3)根据线段上的点到线段的两端点的距离的和等线段的距离,可得答案;
(4)根据线段上的点到线段的两端点的距离的和等线段的距离,可得答案.
(2)根据数轴上两点间的距离是大数减小数,可得答案;
(3)根据线段上的点到线段的两端点的距离的和等线段的距离,可得答案;
(4)根据线段上的点到线段的两端点的距离的和等线段的距离,可得答案.
解答:解:(1)数轴上表示1和5两点之间的距离是 4,数轴上表示2和-1的两点之间的距离是 3;
(2)数轴上表示x和-1的两点之间的距离表示为|x+1|;
(3)若x表示一个有理数,且-4<x<2,则|x-2|-|x+4|=6;
(4)|x+3|+|x+4|最小=1,x=-3,x=-4.
故答案为:4,3,|x+1|,6,1,x=-3,x=-4.
(2)数轴上表示x和-1的两点之间的距离表示为|x+1|;
(3)若x表示一个有理数,且-4<x<2,则|x-2|-|x+4|=6;
(4)|x+3|+|x+4|最小=1,x=-3,x=-4.
故答案为:4,3,|x+1|,6,1,x=-3,x=-4.
点评:本题考查了数轴,利用了两点间的距离公式,线段上的点到线段的两端点的距离的和等线段的距离.

练习册系列答案
相关题目
已知
-1的整数部分为a,小数部分为b,则(
+a)(b+1)=( )
| 11 |
| 11 |
| A、5 | B、6 | C、7 | D、8 |
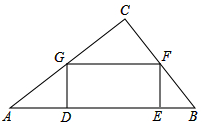 内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.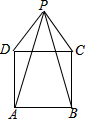 如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形.
如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形. 如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为
如图,在△ABC中,AB=2014,AC=2012,AD为中线,则△ABD与△ACD的周长之差为