题目内容
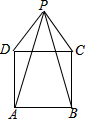 如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形.
如图,P为正方形ABCD外一点,且∠PAD=∠PBC=15°,求证:△PDC为等边三角形.考点:正方形的性质,等边三角形的判定
专题:证明题
分析:在△PAB内部作∠PAE=∠PBE=15°,连接PE,求出∠ABE=∠BAE=60°,判断出△ABE是等边三角形,再根据等边三角形和等腰三角形的对称性求出∠PEA=150°,利用“边角边”证明△PAD和△PAE全等,根据全等三角形对应角相等可得∠PDA=∠PEA,再求出∠PDC=60°,同理可得∠PCD=60°,然后根据等边三角形的判定方法证明即可.
解答: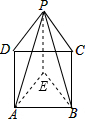 证明:如图,在△PAB内部作∠PAE=∠PBE=15°,连接PE,
证明:如图,在△PAB内部作∠PAE=∠PBE=15°,连接PE,
∵∠PAD=∠PBC=15°,
∴∠ABE=∠BAE=90°-15°×2=60°,
∴△ABE是等边三角形,
∴AE=AB=AD,∠AEB=60°,
∵∠PAB=∠PBA=90°-15°=75°,
∴PA=PB,
∴PE在AB的垂直平分线上,
∴∠PEA=
(360°-60°)=150°,
在△PAD和△PAE中,
,
∴△PAD≌△PAE(SAS),
∴∠PDA=∠PEA=150°,
∴∠PDC=150°-90°=60°,
同理可得∠PCD=60°,
∴△PDC为等边三角形.
 证明:如图,在△PAB内部作∠PAE=∠PBE=15°,连接PE,
证明:如图,在△PAB内部作∠PAE=∠PBE=15°,连接PE,∵∠PAD=∠PBC=15°,
∴∠ABE=∠BAE=90°-15°×2=60°,
∴△ABE是等边三角形,
∴AE=AB=AD,∠AEB=60°,
∵∠PAB=∠PBA=90°-15°=75°,
∴PA=PB,
∴PE在AB的垂直平分线上,
∴∠PEA=
| 1 |
| 2 |
在△PAD和△PAE中,
|
∴△PAD≌△PAE(SAS),
∴∠PDA=∠PEA=150°,
∴∠PDC=150°-90°=60°,
同理可得∠PCD=60°,
∴△PDC为等边三角形.
点评:本题考查了正方形的性质,等边三角形的判定与性质,难点在于作辅助线构造出等边三角形和全等三角形.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 在三角形纸片ABC中,底角∠A=30°,将纸片的一角对折,使点A落在△ABC内,若∠2=20°,则∠1=
在三角形纸片ABC中,底角∠A=30°,将纸片的一角对折,使点A落在△ABC内,若∠2=20°,则∠1=