题目内容
某工厂三个车间六月份共生产零件651个，第二车间生产的零件数比第三车间生产的零件数多10%，第一车间生产的零件数比第二车间生产的零件数多5%，求三个车间各生产多少个零件？
考点：一元一次方程的应用
专题：
分析：设第三车间生产的零件数为x个，表示出第二车间和第一车间生产的零件数，再根据三个车间生产的零件数列出方程求解即可．
解答：解：设第三车间生产的零件数为x个，
则第二车间生产的零件数为（1+10%）x=1.1x，第一车间生产的零件数为（1+5%）×1.1x=1.155x，
由题意得，x+1.1x+1.155x=651，
解得x=200，
1.1x=1.1×200=220，
1.155x=1.155×200=231，
答：三个车间各生产231个，220个，200个零件．
则第二车间生产的零件数为（1+10%）x=1.1x，第一车间生产的零件数为（1+5%）×1.1x=1.155x，
由题意得，x+1.1x+1.155x=651，
解得x=200，
1.1x=1.1×200=220，
1.155x=1.155×200=231，
答：三个车间各生产231个，220个，200个零件．
点评：本题考查了一元一次方程的应用，用第三车间的零件个数表示出另两个车间生产的零件个数是解题的关键．
练习册系列答案
相关题目
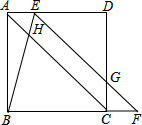如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连接EF与边CD相交于点G，连接BE与对角线AC相交于点H，AE=CF，BE=EG．
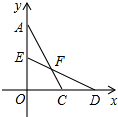平面直角坐标系中，将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起，相交于点F．
在三角形纸片ABC中，底角∠A=30°，将纸片的一角对折，使点A落在△ABC内，若∠2=20°，则∠1=
