题目内容
19. 已知BD为△ABC中线,CF∥BD,EF交BD于G,若BG=EG,BD=2,EF=3,求CF的长.
已知BD为△ABC中线,CF∥BD,EF交BD于G,若BG=EG,BD=2,EF=3,求CF的长.
分析 延长AB交CF的延长线于点Q,根据BD为△ABC中线,CF∥BD,可得出BD为△ACQ的中位线,得BD=$\frac{1}{2}$CQ,由平行线的性质得出∠EBD=∠EQC,从而得出∠E=∠Q,根据等角对等边得出CF的长.
解答 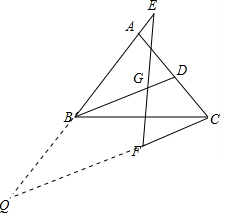 解:延长AB交CF的延长线于点Q,
解:延长AB交CF的延长线于点Q,
∵BD为△ABC中线,CF∥BD,
∴BD为△ACQ的中位线,
∴BD=$\frac{1}{2}$CQ,
∵BD=2,
∴CQ=4,
∵CF∥BD,∠EBD=∠EQC,
∵BG=EG,
∴∠E=∠EBD,
∴∠E=∠Q,
∴FE=FQ,
∵EF=3,
∴FQ=3,
∴CF=CQ-FQ=4-3=1.
点评 本题考查了相似三角形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.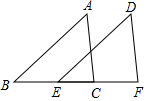 如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )
如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )
①AC=DF ②∠A=∠D ③AC∥DF ④∠A+∠B=∠D+∠DEF.
 如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )
如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )①AC=DF ②∠A=∠D ③AC∥DF ④∠A+∠B=∠D+∠DEF.
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
 如图,AD=AE,∠1=∠2,试说明:BE=CD.
如图,AD=AE,∠1=∠2,试说明:BE=CD. 如图,已知AB=AC,CE⊥AB,BF⊥AC.求证:BF=CE.
如图,已知AB=AC,CE⊥AB,BF⊥AC.求证:BF=CE.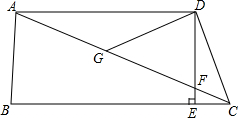 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.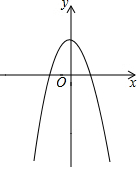 如图,已知二次函数y=-x2+c的图象经过点A(-2,0).
如图,已知二次函数y=-x2+c的图象经过点A(-2,0).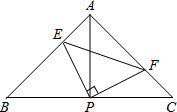 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论: