题目内容
14.若分式$\frac{{m}^{2}-{n}^{2}}{{m}^{2}+mn}=2$,则$\frac{n}{m}$的值等于-1.分析 把分子、分母分解因式,进行约分,即可解答.
解答 解:$\frac{{m}^{2}-{n}^{2}}{{m}^{2}+mn}=2$,
$\frac{(m-n)(m+n)}{m(m+n)}=2$
$\frac{m-n}{m}=2$
$1-\frac{n}{m}=2$
$\frac{n}{m}=-1$,
故答案为:-1.
点评 本题考查了分式的值,解决本题的关键是把分子、分母分解因式,进行约分.

练习册系列答案
相关题目
19.下列说法正确的个数为( )
①$\frac{1}{16}$的平方根是±4;
②-9的算术平方根是+3;
③$\sqrt{36}$的平方根是±6;
④$\sqrt{11}$是11的算术平方根;
⑤36的平方根是-6.
①$\frac{1}{16}$的平方根是±4;
②-9的算术平方根是+3;
③$\sqrt{36}$的平方根是±6;
④$\sqrt{11}$是11的算术平方根;
⑤36的平方根是-6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
3.y=$\sqrt{x-3}$+$\sqrt{3-x}$+8,则3x+2y的平方根是( )
| A. | 5 | B. | -5 | C. | ±3 | D. | ±5 |
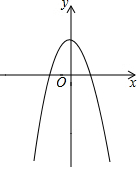 如图,已知二次函数y=-x2+c的图象经过点A(-2,0).
如图,已知二次函数y=-x2+c的图象经过点A(-2,0).