题目内容
14.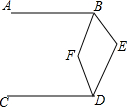 如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.
如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.
分析 首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两只线平行,内错角相等,即可求得∠BFD的度数.
解答 解:过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=$\frac{1}{2}$∠ABE,∠CDF=$\frac{1}{2}$∠CDE,
∴∠ABF+∠CDF=$\frac{1}{2}$(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故答案为125°
点评 此题考查了平行线的性质与角平分线的定义.此题难度适中,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
2.计算(-3)3+52-(-2)2的值为( )
| A. | 2 | B. | -3 | C. | 5 | D. | -6 |
9.要使式子$\sqrt{x-1}$在实数范围内有意义,字母x必须满足的条件是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
19.下列运算正确的是( )
| A. | x4+x4=2x8 | B. | x6÷x2=x3 | C. | (-x5)2=x10 | D. | xm•xn=xmn |
3.在直线AB上取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数( )
| A. | 60° | B. | 90° | C. | 120° | D. | 60°或120° |
 如图,点E是正方形ABCD边BC边的延长线上一点,且CE=$\frac{1}{2}$BC,BG⊥DE于点G,连接AG交CD于点F,BG交CD于点H,AB=$2\sqrt{5}$,则FG的长为$\frac{2\sqrt{2}}{3}$.
如图,点E是正方形ABCD边BC边的延长线上一点,且CE=$\frac{1}{2}$BC,BG⊥DE于点G,连接AG交CD于点F,BG交CD于点H,AB=$2\sqrt{5}$,则FG的长为$\frac{2\sqrt{2}}{3}$. 一只小狗在如图所示的方砖上走动,每块方砖的面积相等,则小狗最终停在阴影方砖上的概率是$\frac{1}{3}$.
一只小狗在如图所示的方砖上走动,每块方砖的面积相等,则小狗最终停在阴影方砖上的概率是$\frac{1}{3}$.