题目内容
5.解下列方程组(1)$\left\{\begin{array}{l}{4x-3y=5}\\{2x-y=2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{4(x-y-1)=3(1-y)-2}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{4x-3y=5①}\\{2x-y=2②}\end{array}\right.$,
②×3-①得:2x=1,
解得:x=$\frac{1}{2}$,
把x=$\frac{1}{2}$代入②得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{4x-y=5①}\\{3x+2y=12②}\end{array}\right.$,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若(a+$\sqrt{2}$)2与|b+1-$\sqrt{2}$|互为相反数,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
13.下列叙述正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 三角形的外心到三边的距离相等 | ||
| C. | 三角形的内心到三边的距离相等 | D. | 相等的圆周角所对的弧相等 |
17.下列各组数中,是勾股数的( )
| A. | 12,15,18 | B. | 11,60,61 | C. | 15,16,17 | D. | 12,35,36 |
15.下列运算中正确的是( )
| A. | 2a+3a2=5a3 | B. | (-2a2)3=-8a6 | C. | a2•a3=a6 | D. | a8÷a2=a4 |
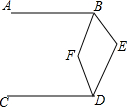 如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.
如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.