题目内容
8.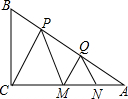 已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求:
已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求:(1)$\frac{AM}{MC}$的值;
(2)AC的长.
分析 (1)过P作PE⊥AC于E,过Q作QF⊥AC于F,由△PCM和△QMN是等边三角形,于是得到∠PCM=∠QMN=60°,证得PC∥QM.同理PM∥QN,推出△AQM∽△APC,求得$\frac{PC}{QM}=\frac{PM}{QN}$=$\frac{1}{3}$,于是得到结论;
(2)由(1)知,$\frac{AM}{AC}=\frac{1}{3}$,同理$\frac{AN}{AM}$=$\frac{1}{3}$,设AN=a,AM=3a,AC=9a,FN=FM=a,得到QF=$\sqrt{3}$a,通过△AFQ∽△ACB,得到$\frac{QF}{BC}=\frac{AF}{AC}$,即可得到结果.
解答 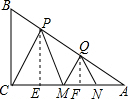 解:(1)过P作PE⊥AC于E,过Q作QF⊥AC于F,
解:(1)过P作PE⊥AC于E,过Q作QF⊥AC于F,
∵△PCM和△QMN是等边三角形,
∴∠PCM=∠QMN=60°,
∴PC∥QM.同理PM∥QN,
∴△AQM∽△APC,
∵△PCM和△QMN是相似比为3:1,
∴$\frac{PC}{QM}=\frac{PM}{QN}$=$\frac{1}{3}$,
∴$\frac{AM}{AC}$=$\frac{QM}{PC}$=$\frac{1}{3}$
∴$\frac{AM}{MC}$=$\frac{1}{2}$;
(2)由(1)知,$\frac{AM}{AC}=\frac{1}{3}$,同理$\frac{AN}{AM}$=$\frac{1}{3}$,
设AN=a,AM=3a,AC=9a,FN=FM=a,
∴QF=$\sqrt{3}$a,
∵∠C=90°,
∴QF∥BC,
∴△AFQ∽△ACB,
∴$\frac{QF}{BC}=\frac{AF}{AC}$,
即$\frac{\sqrt{3}a}{\sqrt{3}}$=$\frac{2a}{9a}$,
∴a=$\frac{2}{9}$,
∴AC=2.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案| A. | 上午12时 | B. | 上午10时 | C. | 上午9时 | D. | 上午8时 |
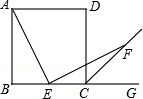 如图,四边形ABCD是正方形,点E在BC上,AE⊥EF,CF是∠DCG的平分线.
如图,四边形ABCD是正方形,点E在BC上,AE⊥EF,CF是∠DCG的平分线. 如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.
如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.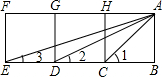 如图,三个正方形拼成一个矩形ABEF.
如图,三个正方形拼成一个矩形ABEF.