题目内容
13.已知关于x的方程x2-2(m+1)x+m2-3=0.(1)当m取何值时,方程有两个不相等的实数根?
(2)设方程的两实数根分别为x1,x2,当(x1+1)(x2+1)=8时,求m的值.
分析 (1)根据判别式的意义得到△=4(m+1)2-4(m2-3)>0,再解不等式即可;
(2)先根据根与系数的关系计算x1+x2,x1•x2的值,而(x1+1)(x2+1)=8,可把x1+x2,x1•x2的值代入,进而可求出m的值.
解答 解:(1)根据题意可知:
△=△=4(m+1)2-4(m2-3)>0,
8m+16>0,
解得m>-2,
当m>-2时,方程有两个不相等的实数根;
(2)∵x2-2(m+1)x+m2-3=0,
∴x1+x2=2(m+1),x1x2=m2-3,
∵(x1+1)(x2+1)=8,
∴x1x2+(x1+x2)+1=8,
∴m2+2m-8=0,
∴m=-4或m=2,
∵m>-2,
∴m=2.
点评 本题考查了根的判别式、根与系数的关系,解题的关键是掌握根的判别式、根与系数的关系的表达式,并会熟练计算.

练习册系列答案
相关题目
3.若(3x2-3x+2)-(-x2+3x-3)=Ax2+Bx+C,则A、B、C的值为( )
| A. | 4,-6,5 | B. | 4,0,-1 | C. | 2,0,5 | D. | 2,-6,-1 |
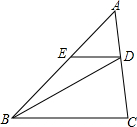 如图,DE∥BC,S△ADE=3,S△CBD=18,求S△ABC.
如图,DE∥BC,S△ADE=3,S△CBD=18,求S△ABC.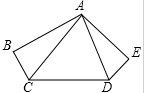 如图,已知AB⊥BC于B,AE⊥DE于E,AB=AE,∠ACB=∠ADE,∠ACD=∠ADC=70°,∠BAD=60°,求∠BAE的度数.
如图,已知AB⊥BC于B,AE⊥DE于E,AB=AE,∠ACB=∠ADE,∠ACD=∠ADC=70°,∠BAD=60°,求∠BAE的度数.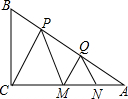 已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求:
已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求: 如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.
如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.