题目内容
20．在Rt△ABC中，∠C=90°，a=5，b=$\sqrt{7}$，求∠A的三个三角函数之比．分析 根据∠C=90°，a=5，b=$\sqrt{7}$，由勾股定理得出c，利用锐角三角函数，tanA=$\frac{a}{b}$，sinA=$\frac{a}{c}$，cosA．
解答 解：∵∠C=90°，
∴a2+b2=c2，
∵a=5，b=$\sqrt{7}$，
∴c=4$\sqrt{2}$，
∴sinA=$\frac{a}{c}$=$\frac{5\sqrt{5}}{8}$，
cosA=$\frac{b}{c}$=$\frac{\sqrt{14}}{8}$，
tanA=$\frac{a}{b}$=$\frac{5\sqrt{7}}{7}$．
点评 本题考查了解直角三角形，直角三角形的两锐角互余，要熟练掌握好边角之间的关系是解题的关键．
练习册系列答案
相关题目
10．
一个物体的三个视图如图所示，则该物体是（ ）
一个物体的三个视图如图所示，则该物体是（ ）| A． | 圆锥 | B． | 球 | C． | 圆柱 | D． | 长方体 |
如图，△ABC中，AB=AC，∠BAC=90°，且EC⊥AC，EC=AD，求证：AE⊥BD．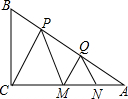
已知，如图，在△ABC中，∠C=90°，BC=$\sqrt{3}$，点P、Q在AB上，点M、N在AC上，且△PCM和△QMN是相似比为3：1的两个等边三角形．求：