题目内容
3. 如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.
如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.
分析 可由题中条件求解△ABE≌△CDF,得出∠BAE=∠DCF,进而可求证AB与CD平行.
解答 证明:∵BE⊥AC于点E,DE⊥AC于点F,
∴∠AEB=∠CFD=90°,
在△ABE与△CDF中,
$\left\{\begin{array}{l}{BE=DF}\\{∠AEB=∠CFD}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠BAE=∠DCF,
∴AB∥CD.
点评 本题主要考查了全等三角形的判定及性质,能够运用其性质解决一些简单的证明问题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
13.科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况如下表:
由这些数据,科学家推测出植物每天高度增长量y是温度x的二次函数,则函数关系式是( )
| 温度x/℃ | … | -4 | -2 | 0 | 2 | 4 | 4.5 | … |
| 植物每天高度增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 19.75 | … |
| A. | y=-x2-2x+49 | B. | y=-x2+2x+49 | C. | y=x2+2x-49 | D. | y=x2-2x+49 |
 如图,△ABC中,AB=AC,∠BAC=90°,且EC⊥AC,EC=AD,求证:AE⊥BD.
如图,△ABC中,AB=AC,∠BAC=90°,且EC⊥AC,EC=AD,求证:AE⊥BD.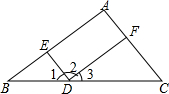 如图,推理填空:
如图,推理填空: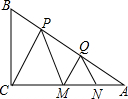 已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求:
已知,如图,在△ABC中,∠C=90°,BC=$\sqrt{3}$,点P、Q在AB上,点M、N在AC上,且△PCM和△QMN是相似比为3:1的两个等边三角形.求: