题目内容
15.先化简,再求值:($\frac{x}{x-1}$+$\frac{2x}{x+1}$)÷$\frac{x}{{x}^{2}-1}$,其中x=$\frac{2}{3}$.分析 根据分式的加法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:($\frac{x}{x-1}$+$\frac{2x}{x+1}$)÷$\frac{x}{{x}^{2}-1}$
=$\frac{x(x+1)+2x(x-1)}{(x+1)(x-1)}•\frac{(x+1)(x-1)}{x}$
=(x+1)+2(x-1)
=x+1+2x-2
=3x-1,
当x=$\frac{2}{3}$时,原式=3×$\frac{2}{3}$-1=2-1=1.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
20.下列各命题不成立的是( )
| A. | 平行四边形的对边平行且相等 | |
| B. | 依次连结正方形各边中点所得的四边形是正方形 | |
| C. | 对角线互相平分且相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
5.某校随机抽查了10名参加2017年我市初中学业水平考试学生的体育成绩,得到的结果如表:
下列说法中,正确的是( )
| 成绩/分 | 56 | 57 | 58 | 59 | 60 |
| 人数 | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名学生体育成绩的中位数为58 | B. | 这10名学生体育成绩的平均数为58 | ||
| C. | 这10名学生体育成绩的众数为60 | D. | 这10名学生体育成绩的方差为60 |
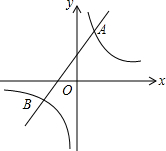 如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点.
如图,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(2,m),B(-3,-2)两点. 一辆货车从A地运货到240km的B地,卸货后返回A地,如图中实线是货车离A地的路程y(km)关于出发后的时间x(h)之间的函数图象.货车出发时,正有一个自行车骑行团在AB之间,距A地40km处,以每小时20km的速度奔向B地.
一辆货车从A地运货到240km的B地,卸货后返回A地,如图中实线是货车离A地的路程y(km)关于出发后的时间x(h)之间的函数图象.货车出发时,正有一个自行车骑行团在AB之间,距A地40km处,以每小时20km的速度奔向B地. 如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是垂线段最短.
如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是垂线段最短.