题目内容
已知∠1与∠2互补,∠2与∠3互补,那么∠1与∠3的关系是( )
| A、相等 | B、互补 |
| C、互余 | D、不能确定 |
考点:余角和补角
专题:
分析:根据同一个角的补角相等,可以等到结论.
解答:解:因为∠1与∠2互补,∠2与∠3互补,
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3,
故选:A.
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3,
故选:A.
点评:本题主要考查补角的相关计算;用到的知识点为:互补的2个角的和是180°.

练习册系列答案
相关题目
若关于x,y的二元一次方程组
的解满足x-y<2,则a的取值范围是( )
|
| A、a>6 | B、a<6 |
| C、a>2 | D、a<2 |
数学表达式①-5<7;②3y-6>0;③a=6;④2x-3y;⑤a≠2;⑥7y-6>y+2,其中是不等式的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知关于x的不等式ax+1>0(a≠0)的解集是x<2,则直线y=ax+1与x轴的交点是( )
| A、(0,2) |
| B、(-1,0) |
| C、(0,-1) |
| D、(2,0) |
方程2x+y=9的正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
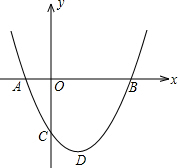 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中: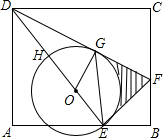 如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F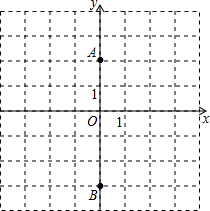 如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.
如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.