题目内容
9.在△ABC中,∠B=30°,AD是BC上的高,且AD2=BD•DC,则∠BCA的度数是60或120度.分析 分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角的相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.
解答 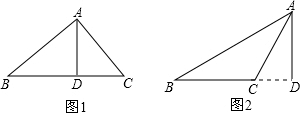 解:当∠BCA为锐角时,如图1所示,
解:当∠BCA为锐角时,如图1所示,
∵AD2=BD•DC,
∴$\frac{AD}{CD}$=$\frac{BD}{AD}$,
又AD⊥BC,
∴∠ADB=∠CDA=90°,
∴△ADB∽△CDA,又∠B=35°,
∴∠CAD=∠B=35°,∠BCA=∠BAD,
在Rt△ADB中,∠ADB=90°,∠B=30°,
∴∠BAD=60°,
则∠BCA=∠BAD=60°;
当∠BCA为钝角时,如图2所示,
同理可得△ADB∽△CDA,又∠B=30°,
可得∠CAD=∠B=30°,
则∠BCA=∠CDA+∠CAD=120°,
综上,∠BCA的度数为60°或120°.
故答案为:60或120.
点评 此题考查了相似三角形的判定与性质,直角三角形的性质,以及外角的性质,利用了分类讨论的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.某商品的标价为每件900元,为了吸引顾客,商店在标价8折的基础上再让利30元销售这种商品,此时仍可获利20%,如果设这种商品的进价为x元,则根据题意,可列出方程为( )
| A. | 20%x-30=900×80%-x | B. | 20%x=900×80%-30-x | ||
| C. | 900×20%=900×80%-x-30 | D. | 900×20%=900×80%+30-x |
4.经过点(-2,1)的反比例函数图象应在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、二象限 |
1.下列方程不是一元二次方程的是( )
| A. | ax+1=x2+x | B. | xy=16 | C. | x2+bx+c=0 | D. | m2=3 |
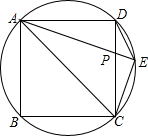 如图,已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,
如图,已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,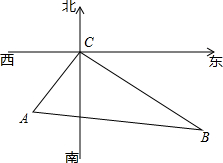 在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?