题目内容
19.如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第3个矩形的面积为$\frac{1}{16}$.
分析 易得第二个矩形的面积为($\frac{1}{2}$)2,第三个矩形的面积为($\frac{1}{2}$)4,依此类推,第n个矩形的面积为($\frac{1}{2}$)2n-2.
解答 解:已知第一个矩形的面积为1;
第二个矩形的面积为原来的($\frac{1}{2}$)2×2-2s=$\frac{1}{4}$;
第三个矩形的面积是($\frac{1}{2}$)2×3-2=$\frac{1}{16}$,
故答案为:$\frac{1}{16}$;
点评 本题考查了三角形的中位线定理及矩形、菱形的性质,是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目
10. 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )
 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
14.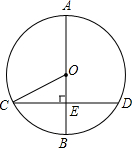 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
11.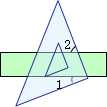 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )| A. | 25° | B. | 65° | ||
| C. | 75° | D. | 以上结果均不正确 |
 在半径为0.5米的圆柱形油罐内装入一些油,截面如图所示,若油面宽AB=0.6米,则油的最大深度是0.1米.
在半径为0.5米的圆柱形油罐内装入一些油,截面如图所示,若油面宽AB=0.6米,则油的最大深度是0.1米.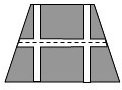 如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?
如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?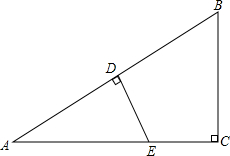 如图,在Rt△ABC中,AC=10,BC=6,∠C=90°,D为AB中点,DE⊥AB于D交AC于E,求CE长.
如图,在Rt△ABC中,AC=10,BC=6,∠C=90°,D为AB中点,DE⊥AB于D交AC于E,求CE长.