题目内容
14.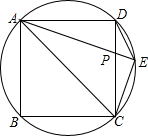 如图,已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,
如图,已知:圆内接正方形ABCD,∠DAC的平分线交圆于E,交CD于P,(1)求证:DE2=AE•EP;
(2)若EP=1,AP=3,求圆的半径r?
分析 (1)根据∠DAC的平分线交圆于E,得到∠DAE=∠CAE,根据圆周角定理得到∠AED=∠DEP,推出△ADE∽△DPE,于是得到$\frac{PE}{DE}=\frac{DE}{AE}$,即可得到结论;
(2)由EP=1,AP=3,得到AE=4,于是得到DE=2根据圆周角定理得到CE=DE=2,由于AC是直径,于是得到∠AEC=90,根据勾股定理得到AC=$\sqrt{A{E^2}+C{E^2}}=2\sqrt{5}$,即可得到结论.
解答 (1)证明:∵∠DAC的平分线交圆于E,
∴∠DAE=∠CAE,
∵∠CDE=∠CAE,
∴∠DAE=∠CDE,
∵∠AED=∠DEP,
∴△ADE∽△DPE,
∴$\frac{PE}{DE}=\frac{DE}{AE}$,
∴DE2=AE•EP;
(2)解:∵EP=1,AP=3,
∴AE=4,
∴DE2=AE•EP=4,
∴DE=2
∵∠DAE=∠CAE,
∴弧DE=弧CE,
∴CE=DE=2,
∵圆内接正方形ABCD,
∴∠ADC=90,
∴AC是直径,
∴∠AEC=90,
∴AC=$\sqrt{A{E^2}+C{E^2}}=2\sqrt{5}$,
∴r=$\sqrt{5}$.
点评 本题考查的是正多边形的圆及相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
4.下列事件中,是不确定事件的是( )
| A. | 明年小刚的年龄比今年大一岁 | B. | 农历的春节在元旦之后 | ||
| C. | 任意买一张电影票座位号是偶数 | D. | 我市冬季的平均温度比夏季低 |
6.下面哪一个运算结果是相等的( )
| A. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ | B. | -22与(-2)2 | C. | -(-1)2011与(-1)2010 | D. | (-5)2与-52 |
 如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1.
如图,直线l:y=kx+b经过A(0,-1)、B(1,0)两点,则关于x的不等式kx+b>0的解集为x>1.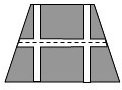 如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?
如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?