题目内容
17.如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )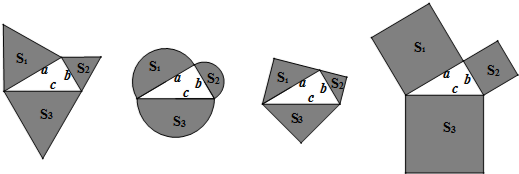
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据直角三角形a、b、c为边,应用勾股定理,可得a2+b2=c2.
(1)第一个图形中,首先根据等边三角形的面积的求法,表示出3个三角形的面积;然后根据a2+b2=c2,可得S1+S2=S3.
(2)第二个图形中,首先根据圆的面积的求法,表示出3个半圆的面积;然后根据a2+b2=c2,可得S1+S2=S3.
(3)第三个图形中,首先根据等腰直角三角形的面积的求法,表示出3个等腰直角三角形的面积;然后根据a2+b2=c2,可得S1+S2=S3.
(4)第四个图形中,首先根据正方形的面积的求法,表示出3个正方形的面积;然后根据a2+b2=c2,可得S1+S2=S3.
解答 解:(1)S1=$\frac{\sqrt{3}}{4}$a2,S2=$\frac{\sqrt{3}}{4}$b2,S3=$\frac{\sqrt{3}}{4}$c2,
∵a2+b2=c2,
∴$\frac{\sqrt{3}}{4}$a2+$\frac{\sqrt{3}}{4}$b2=$\frac{\sqrt{3}}{4}$c2,
∴S1+S2=S3.
(2)S1=$\frac{π}{8}$a2,S2=$\frac{π}{8}$b2,S3=$\frac{π}{8}$c2,
∵a2+b2=c2,
∴$\frac{π}{8}$a2+$\frac{π}{8}$b2=$\frac{π}{8}$c2,
∴S1+S2=S3.
(3)S1=$\frac{1}{4}$a2,S2=$\frac{1}{4}$b2,S3=$\frac{1}{4}$c2,
∵a2+b2=c2,
∴$\frac{1}{4}$a2+$\frac{1}{4}$b2=$\frac{1}{4}$c2,
∴S1+S2=S3.
(4)S1=a2,S2=b2,S3=c2,
∵a2+b2=c2,
∴S1+S2=S3.
综上,可得
面积关系满足S1+S2=S3图形有4个.
故选:D.
点评 (1)此题主要考查了勾股定理的应用,要熟练掌握,解答此题的关键是要明确:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
(2)此题还考查了等腰直角三角形、等边三角形、圆以及正方形的面积的求法,要熟练掌握.

| A. | 开口向上,顶点坐标为(-1,-4) | B. | 开口向下,顶点坐标为(1,4) | ||
| C. | 开口向上,顶点坐标为(1,4) | D. | 开口向下,顶点坐标为(-1,-4) |
| A. | (2mn)2=4m2n2 | B. | (-2mn)2=4m2n2 | C. | (2m2n2)3=8m6n6 | D. | (-2m2n2)3=-8m5n5 |
| A. | m+n | B. | n-m | C. | m-n | D. | -m-n |