题目内容
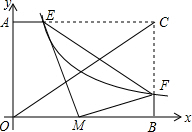 如图,在平面直角坐标系中,矩形AOBC的边OA,OB分别在y轴和x轴上,已知对角线OC=5,tan∠BOC=
如图,在平面直角坐标系中,矩形AOBC的边OA,OB分别在y轴和x轴上,已知对角线OC=5,tan∠BOC=| 3 |
| 4 |
| k |
| x |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
考点:反比例函数综合题
专题:
分析:过点E作ED⊥OB于点D,根据折叠的性质得∠EMF=∠C=90°,EC=EM,CF=DF,易证Rt△MEM∽Rt△BMF;而EC=AC-AE=4-
,CF=BC-BF=3-
,可得
的比值;故可得出EM:MB=ED:MF=4:3,而ED=3,从而求出BM,然后在Rt△MBF中利用勾股定理得到关于k的方程,解方程求出k的值.
| k |
| 3 |
| k |
| 4 |
| EM |
| MF |
解答:
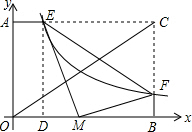 解:过点E作ED⊥OB于点D,
解:过点E作ED⊥OB于点D,
∵对角线OC=5,tan∠BOC=
,
∴BC=3,BO=4,
∵将△CEF沿EF对折后,C点恰好落在OB上的M点处,
∴∠EMF=∠C=90°,EC=EM,CF=MF,
∴∠DME+∠FMB=90°,
而ED⊥OB,
∴∠DME+∠DEM=90°,
∴∠DEM=∠FMB,
∴Rt△DEM∽Rt△BMF;
又∵EC=AC-AE=4-
,CF=BC-BF=3-
,
∴EM=4-
,MF=3-
,
∴
=
=
;
∴ED:MB=EM:MF=4:3,而ED=3,
∴MB=
,
在Rt△MBF中,MF2=MB2+BF2,即(3-
)2=(
)2+(
)2,
解得:k=
,
故选:D.
 解:过点E作ED⊥OB于点D,
解:过点E作ED⊥OB于点D,∵对角线OC=5,tan∠BOC=
| 3 |
| 4 |
∴BC=3,BO=4,
∵将△CEF沿EF对折后,C点恰好落在OB上的M点处,
∴∠EMF=∠C=90°,EC=EM,CF=MF,
∴∠DME+∠FMB=90°,
而ED⊥OB,
∴∠DME+∠DEM=90°,
∴∠DEM=∠FMB,
∴Rt△DEM∽Rt△BMF;
又∵EC=AC-AE=4-
| k |
| 3 |
| k |
| 4 |
∴EM=4-
| k |
| 3 |
| k |
| 4 |
∴
| EM |
| MF |
4-
| ||
3-
|
| 4 |
| 3 |
∴ED:MB=EM:MF=4:3,而ED=3,
∴MB=
| 9 |
| 4 |
在Rt△MBF中,MF2=MB2+BF2,即(3-
| k |
| 4 |
| 9 |
| 4 |
| k |
| 4 |
解得:k=
| 21 |
| 8 |
故选:D.
点评:本题考查的是反比例函数综合题,涉及到反比例函数的性质、反比例函数图象上点的坐标特点,折叠的性质、勾股定理以及三角形相似的判定与性质等知识,难度适中.

练习册系列答案
相关题目
|a-
|+(b+1)2=0,则ab的值是( )
| 1 |
| 2 |
A、-
| ||
B、±
| ||
C、
| ||
D、
|
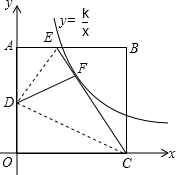 如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=
如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y= 如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是
如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是