题目内容
如图，某水库大坝横截面示意图，其中AB，CD分别表示水库上下底面的水平线，∠ABC=120°，BC的长是50米，则水库大坝的高度h是考点：解直角三角形的应用-坡度坡角问题
专题：
分析：过点C作CE⊥AB延长线于点E，根据∠ABC=120°，可得∠CBE=60°，然后在Rt△BCE中，利用三角函数求出高度h．
解答：
解：过点C作CE⊥AB延长线于点E，
∵∠ABC=120°，
∴∠CBE=60°，
在Rt△BCE中，
∵BC=50米，∠CBE=60°，
∴CE=
=25
（米）．
故答案为：25
．
∵∠ABC=120°，
∴∠CBE=60°，
在Rt△BCE中，
∵BC=50米，∠CBE=60°，
∴CE=
| CE |
| sin60° |
| 3 |
故答案为：25
| 3 |
点评：本题考查了解直角三角形的应用，解答本题的关键是根据坡角构造直角三角形，利用三角函数的知识求解．
练习册系列答案
相关题目
一盏台灯原价是100元，经连续两次升价后，价格变为121元．如果每次升价的百分率是一样的，那么设每次升价的百分率为x，那么x满足方程是（ ）
| A、100（1+x）2=121 |
| B、100（1-x）2=121 |
| C、100（1+2x）=121 |
| D、100（1-2x）=121 |
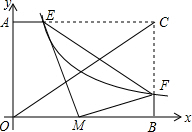如图，在平面直角坐标系中，矩形AOBC的边OA，OB分别在y轴和x轴上，已知对角线OC=5，tan∠BOC=| 3 |
| 4 |
| k |
| x |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
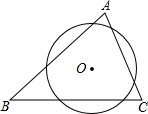如图所示，在△ABC中，∠A=70°，⊙O截△ABC的三条边所得的弦长相等，则∠BOC的度数为（ ）| A、125° | B、130° |
| C、135° | D、160° |
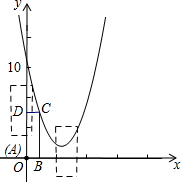在直角坐标系中，抛物线y=x2+bx+c经过点（0，10）和点（4，2）．
如图所示，在直角三角形ABC中，∠ACB=90°，BC=2，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F．若EF=5，则AE=（ ）