题目内容

（1）8a3b2+12ab3c                  
（2）m（a-3）+2（3-a）
（3）-3x2+6xy-3y2                  
（4）（p-4）（p+1）+3p．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式提取公因式即可得到结果；
（2）原式变形后，提取公因式即可得到结果；
（3）原式提取公因式，再利用完全平方公式分解即可；
（4）原式整理后，利用平方差公式分解即可．
解答： 解：（1）原式=4ab2（2a2+3bc）；
（2）原式=（a-3）（m-2）；
（3）原式=-3（x-y）2；
（4）原式=p2-4=（p+2）（p-2）．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠B=50°，∠AEC=80°，CE平分∠ACB，求∠A和∠BCD的度数．
已知关于x的方程：kx2-（k-1）x-1=0（k≠0）
（1）求证：方程总有两个实数根；
（2）若抛物线y=kx2-（k-1）x-1截x轴所得的线段长为3，求k的值．
一盏台灯原价是100元，经连续两次升价后，价格变为121元．如果每次升价的百分率是一样的，那么设每次升价的百分率为x，那么x满足方程是（　　）
A、100（1+x）2=121
B、100（1-x）2=121
C、100（1+2x）=121
D、100（1-2x）=121
已知x1，x2是方程x2-5x=0的两个实数根，则x1+x2的值是
 
．
如图是我市环北路改造后一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为4m，水面最深地方的高度为1m，则该输水管的半径为（　　）
A、2mB、2.5m
C、4mD、5m
计算：|1-
2
|+|
3
-
2
|+|
3
-
4
|
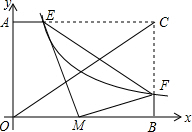如图，在平面直角坐标系中，矩形AOBC的边OA，OB分别在y轴和x轴上，已知对角线OC=5，tan∠BOC=
3
4
．F是BC边上一点，过点F的反比列函数y=
k
x
（k＞0）的图象与AC边交于点E，若将△CEF沿EF翻折后，点C恰好落在OB上的点M处，则k的值为（　　）
A、2
B、
17
5
C、3
D、
21
8
如图所示，在直角三角形ABC中，∠ACB=90°，BC=2，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F．若EF=5，则AE=（　　）
A、2B、3C、4D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网