题目内容
4．若a≠b，则方程（a-b）x2+（c-b）x+c-a=0必有一根是x=-1．分析 将原方程左边因式分解可得（x+1）[（a-b）x+（c-a）]=0，即x+1=0或（a-b）x+（c-a）=0，从而得出答案．
解答 解：∵原方程左边因式分解后可得：（x+1）[（a-b）x+（c-a）]=0，
∴x+1=0或（a-b）x+（c-a）=0，
则方程必有一根为x=-1，
故答案为：x=-1．
点评 本题主要考查一元二次方程的解和街一元二次方程的能力，熟练掌握因式分解法解一元二次方程是解题的关键．
练习册系列答案
相关题目
如图所示是某路灯灯架示意图，其中点A表示电灯，AB和BC为灯架，l表示地面，已知AB=2m，BC=5.7m，∠ABC=100°，BC⊥l于点C，求电灯A距离地面l的高度（结果精确到0.1m，参考数据：sin80°≈0.98，cos80°≈0.17，tan80°≈5.67）．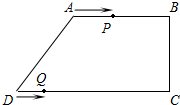
在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，沿折线A-B-C-D方向以2cm/s的速度匀速运动；点Q从点D出发，沿线段DC方向以1cm/s的速度匀速运动，已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为t（s）．
13．
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，连结EB，DE，则下列线段的比值中，一定与CE：BC的比值相等的是（ ）
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，连结EB，DE，则下列线段的比值中，一定与CE：BC的比值相等的是（ ）| A． | DE：AE | B． | BD：AB | C． | AE：AB | D． | CD：BE |
如图，完全一样的矩形的顶点都落在平面直角坐标系中方格的格点处，按照如图所示的方式标注字母．