题目内容
13. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,DE,则下列线段的比值中,一定与CE:BC的比值相等的是( )
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,DE,则下列线段的比值中,一定与CE:BC的比值相等的是( )| A. | DE:AE | B. | BD:AB | C. | AE:AB | D. | CD:BE |
分析 连接AD,根据等腰三角形的三线合一定理和圆周角定理可知∠CBE=∠BAD,从而可证明△CBE∽△BAD,利用相似三角形的性质即可得到答案.
解答  解:连接AD,
解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∵AB=AC,
∴∠BAD=∠CAD
∵$\widehat{DE}=\widehat{DE}$,
∴∠CBE=∠CAD,
∴∠CBE=∠BAD,
∴△CBE∽△BAD,
∴$\frac{CE}{BC}=\frac{BD}{AB}$
故选(B)
点评 本题考查相似三角形的判定,涉及圆周角定理,等腰三角形的性质,相似三角形的性质与判定,综合程度较高,属于中等题型,

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.下列各组中的两项是同类项的是( )
| A. | 3a2b与ab2 | B. | a2b与ba2 | C. | 3ab与a | D. | 2与3x |
1.一次函数y=2x-1的图象经过的象限是( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
8.对于事件“从车间生产的100个(其中有2个是次品)产品中任意抽一个,所抽取的产品是次品”,下列对于该事件的描述正确的是( )
| A. | 该事件是必然事件 | B. | 该事件是不可能事件 | ||
| C. | 该事件是不确定事件 | D. | 该事件发生的可能性很大 |
5.在△ABC中,点D在AB上,点E在AC上,且△ADE与△ABC相似,AD=EC,BD=10,AE=4,则AB的长为( )
| A. | $2\sqrt{10}$ | B. | 12 | C. | 2$\sqrt{10}$+10 | D. | 12或2$\sqrt{10}$+10 |
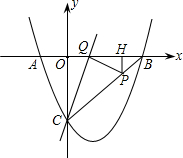 如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.