题目内容
8.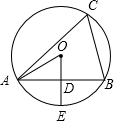 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
分析 根据由垂径定理和圆周角定理知,OD是AB的中垂线,有AE=BE,AD=BD,∠AOD=∠BOD=∠C=60°.利用三角函数可求得AD=AOsin60°=$\sqrt{3}$,OD=OAsin∠AOD=OAsin60°=1,AB=2$\sqrt{3}$,从而判断出选项C是错误的.
解答 解:∵OD⊥AB,
∴AE=BE,AD=BD,∠AOD=∠BOD=∠C=60°.
∴AD=AOsin60°=$\sqrt{3}$,OD=OAsin∠AOD=OAsin60°=1.
∴AB=2$\sqrt{3}$.
∴A,B,D均正确,C错误.
故选C.
点评 本题利用了垂径定理和圆周角定理,直角三角形的性质,锐角三角函数的概念求解.

练习册系列答案
相关题目
18.某班在一次美化校园的劳动中,先安排35人打扫卫生,15人拔草,后又增派10人去支援,结果打扫卫生的人数是拔草人数的2倍,若设支援打扫卫生的同学有x人,则下列方程正确的是( )
| A. | 35+x=2×10 | B. | 35+x=2×(15+10-x) | C. | 35+x=2×(15-x) | D. | 35+x=2×15 |
16. 如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )
如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )
 如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )
如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )| A. | 500•sin55° m | B. | 500•cos55° m | C. | 500•tan55° m | D. | $\frac{50}{cos55°}{m}$ |
13.在平面直角坐标系中,已知点A(0,3),B(1,0),C(0,-2),D(3,4),求过其中三个点的抛物线的顶点坐标是( )
| A. | (-$\frac{7}{5}$,$\frac{4}{15}$) | B. | ($\frac{7}{5}$,-$\frac{4}{15}$) | C. | (-$\frac{7}{5}$,-$\frac{4}{15}$) | D. | ($\frac{7}{5}$,$\frac{4}{15}$) |
20.若三角形的两边长分别是4和6,第三边的长是一元二次方程x2-7x+12=0的一个实数根,则该三角形的周长是( )
| A. | 13 | B. | 14 | C. | 17 | D. | 13或14 |
 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOE=140°,∠COD=30°,求∠AOB的度数.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOE=140°,∠COD=30°,求∠AOB的度数. 如图,已知∠ABC=∠E,∠E+∠AME=180°,BA、EF相交于点M,试判断BC与EF是否平行,并说明理由.
如图,已知∠ABC=∠E,∠E+∠AME=180°,BA、EF相交于点M,试判断BC与EF是否平行,并说明理由. 如图,边长为2的菱形ABCD中,∠BAD=60°,现有∠BFE=30°的三角板△BEF,将△BEF绕B旋转得△BE′F′,BE′,BF′所在直线分别交线段AC于点M,N,若点C关于直线BE′的对称点为C′,当C′N⊥AC时,AN的长为$\sqrt{3}$-1.
如图,边长为2的菱形ABCD中,∠BAD=60°,现有∠BFE=30°的三角板△BEF,将△BEF绕B旋转得△BE′F′,BE′,BF′所在直线分别交线段AC于点M,N,若点C关于直线BE′的对称点为C′,当C′N⊥AC时,AN的长为$\sqrt{3}$-1.