题目内容
18.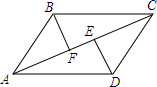 如图,AB=CD,DE⊥AC于E,BF⊥AC于F,且AE=CF,求证:BC=AD,BC∥AD.
如图,AB=CD,DE⊥AC于E,BF⊥AC于F,且AE=CF,求证:BC=AD,BC∥AD.
分析 根据线段的和差得到AF=CE,推出Rt△ABF≌Rt△CDE,由全等三角形的性质得到BF=DE,证得△BCF≌△CDE,根据全等三角形的性质得到BC=AD,∠BCF=∠DAE,根据平行线的判定即可得到结论.
解答 证明:∵AE=CF,
∴AE-EF=CF-EF,
即AF=CE,
∵DE⊥AC于E,BF⊥AC于F,
在Rt△ABF与Rt△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$,
∴Rt△ABF≌Rt△CDE,
∴BF=DE,
在△BCF与△CDE中,
$\left\{\begin{array}{l}{BF=DE}\\{∠BFC=∠DEC=90°}\\{CF=AE}\end{array}\right.$,
∴△BCF≌△CDE,
∴BC=AD,∠BCF=∠DAE,
∴BC∥AD.
点评 本题考查了全等三角形的性质和判定和平行线的性质的应用,注意:全等三角形的判定定理有SAS,AAS,ASA,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.在平行四边形ABCD中,∠A:∠B:∠C=2:1:2,则∠D=( )
| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
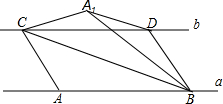 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.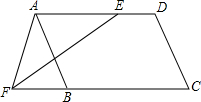 已知:如图,∠A=∠C,∠AEF=∠F.求证:AB∥CD.
已知:如图,∠A=∠C,∠AEF=∠F.求证:AB∥CD. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上)
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上)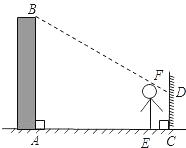 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图,小明边移动边观察,发现站在点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同,此时,小明测得自己落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m).
小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图,小明边移动边观察,发现站在点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同,此时,小明测得自己落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m).