题目内容
7.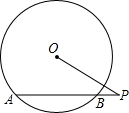 如图,⊙O的半径为3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为( )
如图,⊙O的半径为3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠P=30°,则弦AB的长为( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
分析 连接OA,作OC⊥AB于C,根据垂直定理得到AC=BC,根据直角三角形的性质得到OC=2,根据勾股定理求出AC的长即可得到答案.
解答 解: 连接OA,作OC⊥AB于C,
连接OA,作OC⊥AB于C,
则AC=BC,
∵OP=4,∠P=30°,
∴OC=2,
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{5}$,
∴AB=2AC=2$\sqrt{5}$,
故选:A.
点评 本题考查的是垂直定理和直角三角形的性质,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧、在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
18.下列命题中,是真命题的是( )
| A. | 三角形的外角等于它的两个内角 | |
| B. | 面积相等的两个三角形全等 | |
| C. | 三角形的三条高线相交于三角形内一点 | |
| D. | 成轴对称的两个图形是全等图形 |
15.已知关于x的方程$\frac{2x+m}{x+2}$=3的解是负数,则m的取值范围为( )
| A. | m<6 | B. | m<-2 | C. | m>6 | D. | m<6且m≠4 |
12.阅读下面材料:在数学课上,老师提出如下问题:
小涵的主要作法如下:
老师说:“小涵的做法正确的.”
请回答:小涵的作图依据是直径所对的圆周角是直角.
尺规作图,过圆外一点作圆的切线.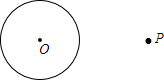 已知:⊙O和点P 求过点P的⊙O的切线 |
| 如图,(1)连结OP,作线段OP的中点A; (2)以A为圆心,OA长为半径作圆,交⊙O于点B,C; (3)作直线PB和PC. 所以PB和PC就是所求的切线.  |
请回答:小涵的作图依据是直径所对的圆周角是直角.
19. 石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )
石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )
 石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )
石墨烯(Graphene)是从石墨材料中剥离出来、由碳原子组成的只有一层原子厚度的二维晶体.石墨烯一层层叠起来就是石墨,厚1毫米的石墨大约包含300万层石墨烯.300万用科学记数法表示为( )| A. | 300×104 | B. | 3×105 | C. | 3×106 | D. | 3000000 |
17.将抛物线y=-(x+1)2向左平移1个单位后,得到的抛物线的顶点坐标是( )
| A. | (-2,0) | B. | (0,0) | C. | (-1,-1) | D. | (-2,-1) |
 如图,在平面直角坐标系中,点P、Q在函数y=$\frac{12}{x}$(x>0)的图象上,PA、QB分别垂直x轴于点A、B,PC、QD分别垂直y轴于点C、D.设点P的横坐标为m,点Q的纵坐标为n,△PCD的面积为S1,△QAB的面积为S2.
如图,在平面直角坐标系中,点P、Q在函数y=$\frac{12}{x}$(x>0)的图象上,PA、QB分别垂直x轴于点A、B,PC、QD分别垂直y轴于点C、D.设点P的横坐标为m,点Q的纵坐标为n,△PCD的面积为S1,△QAB的面积为S2.