题目内容
18. 如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问:
如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问:(1)若AC=16,求MN的长;
(2)若AC=a,则MN=$\frac{1}{2}$a.
分析 (1)根据线段中点的性质,可得MB、NB的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MB、NB的长,根据线段的和差,可得答案.
解答 解:(1)由点M为线段AB的中点,点N为线段BC的中点,得
MB=$\frac{1}{2}$AB,NB=$\frac{1}{2}$BC.
由线段的和差,得
MN=MB+NB=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$×16=8;
(2)由点M为线段AB的中点,点N为线段BC的中点,得
MB=$\frac{1}{2}$AB,NB=$\frac{1}{2}$BC.
由线段的和差,得
MN=MB+NB=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$a.
故答案为:$\frac{1}{2}$a.
点评 本题考查了两点间的距离,利用了线段中点的性质,利用线段的和差得出MN=MB+NB=$\frac{1}{2}$(AB+BC)是解题关键.

练习册系列答案
相关题目
6.以下列各组线段为边作三角形,不能构成直角三角形的是( )
| A. | 2,3,4 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 5,12,13 | D. | 6,8,10 |
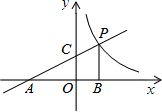 如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9.
如图,直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、C两点,且与双曲线$y=\frac{k}{x}$在第一象限交于点P,作PB⊥x轴于B,S△ABP=9. 下面有一数值转换器,原理如图所示,若开始输入的x的值是22,则第1次输出的结果是11,第2次输出的结果是16,依次继续下去,则第2015次输出的结果是2.
下面有一数值转换器,原理如图所示,若开始输入的x的值是22,则第1次输出的结果是11,第2次输出的结果是16,依次继续下去,则第2015次输出的结果是2. 已知:在△ABC中,∠A=60°,∠B=45°,AB=2.求△ABC的面积(结果可保留根号).
已知:在△ABC中,∠A=60°,∠B=45°,AB=2.求△ABC的面积(结果可保留根号).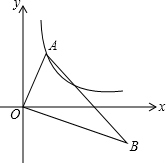 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.