题目内容
7.已知点P(0,a)(a为常数),点Q是抛物线y=$\frac{1}{4}$x2上任意一点.(1)当a=1时,求线段PQ的最小值;
(2)当a>0时,求线段PQ的最小值.
分析 设Q(m,$\frac{1}{4}$m2),
(1)根据勾股定理得出PQ2=(m-0)2+($\frac{1}{4}$m2-1)2=$\frac{1}{16}$m4+$\frac{1}{2}$m2+1,即可求得当m=0时,PQ2的最小值是1,即PQ的最小值是1;
(2)根据勾股定理得出PQ2=(m-0)2+($\frac{1}{4}$m2-a)2=$\frac{1}{16}$m4+(1-$\frac{1}{2}$a)m2+a2,即可求得当m=0时,PQ2的最小值是a2,即PQ的最小值是a.
解答 解:设Q(m,$\frac{1}{4}$m2),
(1)∵P(0,1),
∴PQ2=(m-0)2+($\frac{1}{4}$m2-1)2=$\frac{1}{16}$m4+$\frac{1}{2}$m2+1,
∴当m=0时,PQ2的最小值是1,
∴PQ的最小值是1;
(2)∵P(0,a),
∴PQ2=(m-0)2+($\frac{1}{4}$m2-a)2=$\frac{1}{16}$m4+(1-$\frac{1}{2}$a)m2+a2,
∴当m=0时,PQ2的最小值是a2,
∵a>0,
∴PQ的最小值是a.
点评 本题考查了二次函数图象上点的坐标特征,勾股定理的应用,根据题意设出Q点的坐标,然后根据勾股定理得出PQ关于m的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问:
如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问: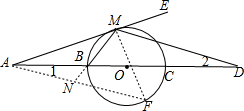 如图,在同一直线上顺次取AB=BC=CD,以BC为直径作⊙O,从A点作⊙O的切线AE,切点为M,求证:∠AMB=∠EMD.
如图,在同一直线上顺次取AB=BC=CD,以BC为直径作⊙O,从A点作⊙O的切线AE,切点为M,求证:∠AMB=∠EMD.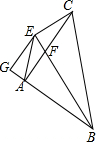 如图,△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于F,CE⊥BF于E,EG⊥AB于G,连AE.下列结论:①AB+AF=BC;②BF=2CE;③FC=GE;④∠GEA=∠CBF.其中正确的有( )
如图,△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于F,CE⊥BF于E,EG⊥AB于G,连AE.下列结论:①AB+AF=BC;②BF=2CE;③FC=GE;④∠GEA=∠CBF.其中正确的有( )