题目内容
3.在等腰直角三角形ABC中,∠C=90°,AC=10,D是AC上一点,若tan∠DBC=$\frac{1}{5}$,求AD的长.分析 利用等腰直角三角形的性质得BC=AC=10,再在Rt△BCD中,利用正切的定义得到tan∠DBC=$\frac{CD}{BC}$,则可计算出CD=2,然后计算AC-CD即可.
解答 解:如图,
∵△ABC为等腰直角三角形,
∴BC=AC=10,
在Rt△BCD中,∵tan∠DBC=$\frac{CD}{BC}$,
∴CD=$\frac{1}{5}$×10=2,
∴AD=AC-CD=10-2=8.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和三角函数的定义进行计算.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
14.A、B两地相距870千米,有两列火车同时从两站相对开出,甲车每小时行60千米,乙车每小时比甲车快5千米,6小时后两车的距离为( )
| A. | 80千米 | B. | 90千米 | C. | 100千米 | D. | 120千米 |
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4.
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是4≤t≤2$\sqrt{5}$或-2$\sqrt{5}$≤t≤-4. 已知一次函数y=kx+b的图象如图所示,
已知一次函数y=kx+b的图象如图所示, 如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问:
如图,点B为线段AC上任一点,点M为线段AB的中点,点N为线段BC的中点,问: 如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.
如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.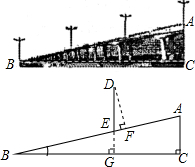 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).