题目内容
14.解方程(1)(x-3)(2x+5)=10
(2)x(2x+3)=4x+6.
分析 (1)先去括号,然后整理得到2x2-x-10=0,再利用因式分解法解方程即可;
(2)先去括号,然后整理得到2x2-x-6=0,再利用因式分解法解方程即可.
解答 解:(1)∵(x-3)(2x+5)=10,
∴2x2-x-10=0,
∴(2x-5)(x+2)=0,
∴2x-5=0或x+2=0,
∴x1=$\frac{5}{2}$,x2=-2;
(2)∵x(2x+3)=4x+6,
∴2x2-x-6=0,
∴(2x+3)(x-2)=0,
∴2x+3=0或x-2=0,
∴x1=-$\frac{3}{2}$,x2=2.
点评 本题考查了因式分解法解一元二次方程的解法的知识,解答本题的关键是掌握因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
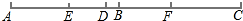 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.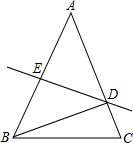 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,若AC=7,BC=5,则BD+DE=$\frac{\sqrt{51}}{2}$+5.
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,若AC=7,BC=5,则BD+DE=$\frac{\sqrt{51}}{2}$+5.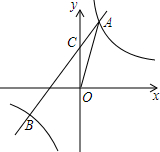 如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.
如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.