题目内容
6.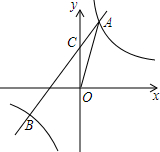 如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.
如图,反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n ),一次函数图象与y轴的交点为C.(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
分析 (1)首先由反比例函数的解析式分别求得m、n的值,再进一步根据点A、B的坐标求得一次函数的解析式;
(2)根据(1)中求得的解析式,令x=0,即可求得点C的坐标;
(3)根据点A、C的坐标即可求得OC=1,OC边上的高是点A的横坐标,进一步求得三角形的面积.
解答 解:(1)由题意,把A(m,2),B(-2,n)代入y=$\frac{2}{x}$中,得$\left\{\begin{array}{l}{m=1}\\{n=-1}\end{array}\right.$,
∴A(1,2),B(-2,-1)将A、B代入y=kx+b中得:
$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数解析式为:y=x+1;
(3)由(1)可知:当x=0时,y=1,
∴C(0,1);
作AD⊥y轴于D,作BE⊥y轴于E.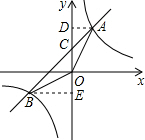
对于一次函数y=x+1,当x=0时,y=1,
∴C(0,1),
∵S△A0B=S△A0C+S△BOC,
∴S△A0B=$\frac{1}{2}$OC×AD+$\frac{1}{2}$OC×BE,
=$\frac{1}{2}$×1×(1+2),
=1.5.
点评 本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,是基础知识要熟练掌握.

练习册系列答案
相关题目
18.在有理数中,有( )
| A. | 最大的数 | B. | 最小的数 | ||
| C. | 绝对值最大的数 | D. | 既不是正数,也不是负数的数 |
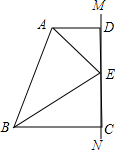 如图,AD∥BC,∠ABC与∠BAD的平分线BE、AE相交于点E,过点E作直线MN⊥AD,交AD于点D,交BE于点C,试判断CE和DE的大小关系,并说明理由.
如图,AD∥BC,∠ABC与∠BAD的平分线BE、AE相交于点E,过点E作直线MN⊥AD,交AD于点D,交BE于点C,试判断CE和DE的大小关系,并说明理由.