题目内容
 如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为
如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为考点:三角形的面积
专题:
分析:作DF⊥AB于F,EG⊥AB于G,从而求得DF∥EG,根据平行线分线段成比例定理求得
=
,得出3EG=DF,然后根据三角形面积公式即可求得.
| EG |
| DF |
| EC |
| DC |
解答: 解:作DF⊥AB于F,EG⊥AB于G,
解:作DF⊥AB于F,EG⊥AB于G,
∴DF∥EG,
∴
=
,
∵DE=2EC,
∴EC:DC=1:3,
∴3EG=DF,
∵
BC•DF=2,AC=BC,
∴
AC•3EG=2,
∴
AC•EG=
,
即△ACE的面积为
.
故答案为
.
 解:作DF⊥AB于F,EG⊥AB于G,
解:作DF⊥AB于F,EG⊥AB于G,∴DF∥EG,
∴
| EG |
| DF |
| EC |
| DC |
∵DE=2EC,
∴EC:DC=1:3,
∴3EG=DF,
∵
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
即△ACE的面积为
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评:本题考查了三角形面积公式的应用,作出辅助线求得两直线平行是本题的关键.

练习册系列答案
相关题目
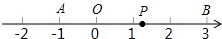 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.

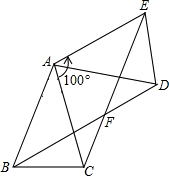 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F. 如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.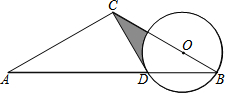 如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.