题目内容
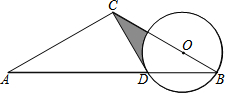 如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.(1)试判断CD与AC的位置关系,并证明;
(2)若△ACB∽△CDB,且AC=3,求图中阴影部分的面积.
考点:切线的判定,扇形面积的计算,相似三角形的判定与性质
专题:计算题
分析:(1)连结OD,如图,由OD=OB得∠ODB=∠B,由AC=CB得∠A=∠B,则∠A=∠ODB,于是可判断OD∥AC,根据平行线的性质得∠ACD=∠ODC,再根据切线的性质得∠ODC=90°,则∠DCA=90°,所以CD⊥AC;
(2)根据相似三角形的性质,由△ACB∽△CDB得到∠BCD=∠A,理由三角形外角性质易得∠ADC=2∠B,则∠ADC=2∠A,再利用三角形内角和定理得∠A+∠ADC=90°,可计算出∠A=30°,则∠CDB=∠B=30°,∠COD=60°,根据含30度的直角三角形三边的关系,在Rt△ACD中可计算出CD=
AC=
,再在Rt△ODC中计算出OD=
CD=1,然后利用三角形的面积减去扇形的面积可得到图中阴影部分的面积.
(2)根据相似三角形的性质,由△ACB∽△CDB得到∠BCD=∠A,理由三角形外角性质易得∠ADC=2∠B,则∠ADC=2∠A,再利用三角形内角和定理得∠A+∠ADC=90°,可计算出∠A=30°,则∠CDB=∠B=30°,∠COD=60°,根据含30度的直角三角形三边的关系,在Rt△ACD中可计算出CD=
| ||
| 3 |
| 3 |
| ||
| 3 |
解答:解:(1)CD⊥AC.理由如下:
连结OD,如图,
∵OD=OB,
∴∠ODB=∠B,
∵AC=CB,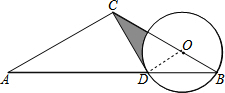
∴∠A=∠B,
∴∠A=∠ODB,
∴OD∥AC,
∴∠ACD=∠ODC,
∵CD是⊙O切线,
∴∠ODC=90°,
∴∠DCA=90°,
∴CD⊥AC;
(2)∵△ACB∽△CDB,
∴∠BCD=∠A,
∴∠ADC=2∠B,
而∠A=∠B,
∴∠ADC=2∠A,
∵∠A+∠ADC=90°,
∴∠A=30°,
∴∠CDB=∠B=30°,
∴∠COD=60°,
在Rt△ACD中,CD=
AC=
,
在Rt△ODC中,OD=
CD=1,
∴图中阴影部分的面积=
×1×
-
=
-
.
连结OD,如图,
∵OD=OB,
∴∠ODB=∠B,
∵AC=CB,

∴∠A=∠B,
∴∠A=∠ODB,
∴OD∥AC,
∴∠ACD=∠ODC,
∵CD是⊙O切线,
∴∠ODC=90°,
∴∠DCA=90°,
∴CD⊥AC;
(2)∵△ACB∽△CDB,
∴∠BCD=∠A,
∴∠ADC=2∠B,
而∠A=∠B,
∴∠ADC=2∠A,
∵∠A+∠ADC=90°,
∴∠A=30°,
∴∠CDB=∠B=30°,
∴∠COD=60°,
在Rt△ACD中,CD=
| ||
| 3 |
| 3 |
在Rt△ODC中,OD=
| ||
| 3 |
∴图中阴影部分的面积=
| 1 |
| 2 |
| 3 |
| 60•π•12 |
| 360 |
| ||
| 2 |
| π |
| 6 |
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了扇形的面积计算和相似三角形的性质.

练习册系列答案
相关题目
下列语句叙述正确的是( )
| A、对于任意有理数,若a≠0,b≠0,则a+b≠0 |
| B、对于任意有理数,若|a|=|b|,则a+b=0 |
| C、对于任意有理数,若a+b=0,|a|=|b| |
| D、两个有理数的和为正数,这两个数一定为正 |
 如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为
如图,点C是线段AB的中点,点E是线段CD上一点,连接AE,若DE=2EC,△BCD的面积为2,则△ACE的面积为 如图,四边形ABCD中,∠B=∠C=90°,AM、DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为
如图,四边形ABCD中,∠B=∠C=90°,AM、DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为 如图,从A到B有三条路径,最短的路径是③,理由是
如图,从A到B有三条路径,最短的路径是③,理由是 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(