Question

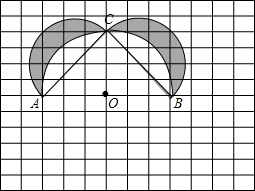如图，在12×12的正方形网格中，每个小正方形的边长为1，在AB的同侧分别以△ABC的三边为直径作三个半圆围成图中的阴影部分，点O为AB的中点（各点都在格点上）．
（1）图中的△ABC的形状是

 

；
（2）图中的阴影部分的面积为

 

；
（3）作出阴影部分关于直线AB的对称图形．

Answer 1

考点：利用轴对称设计图案

专题：

分析：（1）利用勾股定理得出AC=BC，进而得出答案；
（2）利用两小半圆的面积加上△ABC的面积，再减去半圆O的面积，进而得出答案；
（3）利用轴对称图形的性质得出即可．

解答：解：（1）如图所示：AC=BC=

32+42

=5，
故△ABC是等腰三角形；
故答案为：等腰三角形；

（2）图中的阴影部分的面积为：
π×（

1

2

AC）²+

1

2

×AC×BC-

1

2

π×（

1

2

AB）²
=

25π

4

+

25

2

-

9

2

π
=

7

4

π+

25

2

；
故答案为：

7

4

π+

25

2

；

（3）如图所示：阴影部分即为所求．

点评：此题主要考查了圆的面积公式应用以及勾股定理和利用轴对称设计图案，正确利用轴对称图形的定义得出是解题关键．