题目内容
一艘船航行于A、B两个码头之间顺水航行需要2小时,逆水航行需要4小时,已知水流速度是4千米/时,求这两个码头之间的距离.
考点:一元一次方程的应用
专题:
分析:根据船在静水中的速度得到等量关系为:航程÷顺水时间-水流速度=航程÷逆水时间+水流速度,把相关数值代入即可求出答案.
解答:解:设A、B两码头之间的距离是x千米,根据题意得:
-4=
+4,
解得x=32.
答:A、B两码头间距离是32千米.
| x |
| 2 |
| x |
| 4 |
解得x=32.
答:A、B两码头间距离是32千米.
点评:此题考查一元一次方程的应用,求出船在静水中的速度的等量关系是解决本题的关键.

练习册系列答案
相关题目
已知P为△ABC的边AB上的点,且AP2+BP2+CP2-2AP-2BP-2CP+3=0,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
用平面去截一个几何体,得到的截面是一个三角形,则该几何体不可能是( )
| A、长方体 | B、棱柱 | C、圆锥 | D、球 |
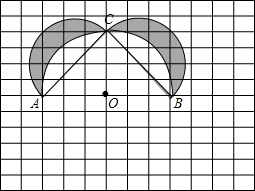 如图,在12×12的正方形网格中,每个小正方形的边长为1,在AB的同侧分别以△ABC的三边为直径作三个半圆围成图中的阴影部分,点O为AB的中点(各点都在格点上).
如图,在12×12的正方形网格中,每个小正方形的边长为1,在AB的同侧分别以△ABC的三边为直径作三个半圆围成图中的阴影部分,点O为AB的中点(各点都在格点上).