题目内容
已知∠AOB=30°，∠BOC=70°，则∠AOC= °．
考点：角的计算
专题：分类讨论
分析：本题是角的计算的多解问题，求解时要注意分情况讨论，可以根据OA在∠BOC的位置关系分为OA在∠BOC的内部和外部两种情况求解．
解答：
解：①如图1，当OA在∠BOC内部，
∵∠AOB=30°，∠BOC=70°，
∴∠AOC=∠BOC-∠AOB=40°；
②如图2，当OA在∠BOC外部，
∵∠AOB=30°，∠BOC=70°，
∴∠AOC=∠AOB+∠BOC=100°；
综上所述，∠AOC为40°或100°．
故答案是：40°或100°．
解：①如图1，当OA在∠BOC内部，∵∠AOB=30°，∠BOC=70°，
∴∠AOC=∠BOC-∠AOB=40°；
②如图2，当OA在∠BOC外部，
∵∠AOB=30°，∠BOC=70°，
∴∠AOC=∠AOB+∠BOC=100°；
综上所述，∠AOC为40°或100°．
故答案是：40°或100°．
点评：本题只是说出了两个角的度数，而没有指出OC与∠AOB的位置关系，因此本题解题的关键是根据题意准确画出图形．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
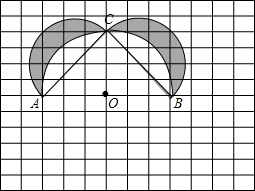如图，在12×12的正方形网格中，每个小正方形的边长为1，在AB的同侧分别以△ABC的三边为直径作三个半圆围成图中的阴影部分，点O为AB的中点（各点都在格点上）．
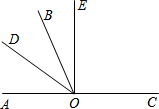如图所示，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，∠BOE=用平面去截一个几何体，得到的截面是一个三角形，则该几何体不可能是（ ）
| A、长方体 | B、棱柱 | C、圆锥 | D、球 |
已知∠AOB=50°，以O为顶点作∠COB=30°，则∠AOC的度数是（ ）
| A、80° |
| B、20° |
| C、20°或50° |
| D、20°或80° |
