题目内容
若3（a2+b2+c2）=（a+b+c）2，则a，b，c三者的关系为（ ）
| A、a+b=b-c |
| B、a+b+c=1 |
| C、a=b=c |
| D、ab=bc=ca |
考点：因式分解的应用
专题：
分析：根据完全平方公式，可得答案．
解答：解：3（a2+b2+c2）=（a+b+c）2，得
3a2+3b2+3c2=a2+b2+c2+2ab+2ac+2bc，
（a-b）2+（b-c）2+（c-a）2=0．
即a=b=c．
故选：C．
3a2+3b2+3c2=a2+b2+c2+2ab+2ac+2bc，
（a-b）2+（b-c）2+（c-a）2=0．
即a=b=c．
故选：C．
点评：本题考查了因式分解，利用了完全平方公式，非负数的和等于零得出每个非负数等于零是解题关键．
练习册系列答案
相关题目
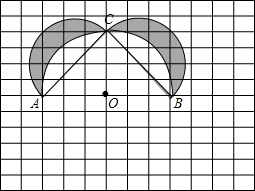如图，在12×12的正方形网格中，每个小正方形的边长为1，在AB的同侧分别以△ABC的三边为直径作三个半圆围成图中的阴影部分，点O为AB的中点（各点都在格点上）．
如图，一根2.5米长的竹竿AB斜靠在竖直的墙AC上，这时B到墙底端为0.7米，如果竹竿的底端沿地面向外滑动0.8米，那么点A将向下移动多少米？化简x-2（x-y）的结果是（ ）
| A、-x+y | B、-x-y |
| C、-x+2y | D、-x-2y |
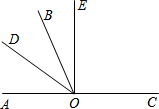如图所示，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，∠BOE=用平面去截一个几何体，得到的截面是一个三角形，则该几何体不可能是（ ）
| A、长方体 | B、棱柱 | C、圆锥 | D、球 |