题目内容
 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E.(1)若CD=3
| 2 |
(2)求证:BC=AD+AE.
考点:四边形综合题
专题:
分析:(1)连接BP,延长DP交BC于点H,由条件可以得出四边形ABFD为正方形,由正方形的性质就可以得出△PFB≌△PFD,就有∠1=∠2,得出∠1=∠3,就有PB=PC,得出PD=PC,由勾股定理就可以求出结论;
(2)连接DE,由直角三角形的性质就可以得出∠5=∠6,得出PE=PB,就有PC=PE,得出DE=DC,证明△DAE≌△DFC就可以得出AE=CF而得出结论.
(2)连接DE,由直角三角形的性质就可以得出∠5=∠6,得出PE=PB,就有PC=PE,得出DE=DC,证明△DAE≌△DFC就可以得出AE=CF而得出结论.
解答:解:(1)如图,连接BP,延长DP交BC于点H,
∵AD∥BC,
∴∠DAC+∠ABC=180°.
∵∠ABC=90°,
∴∠DAB=90°.
∵DF⊥BC,
∴∠DFB=∠DFC=90°
∴∠DAB=∠ABC=∠DFB=90°,
∴四边形ABFD是矩形.
∵AD=AB,
∴矩形ABFD是正方形,
∴AB=BF=DF=AD,∠
∴∠DF⊥BC,AD=AB,∠DAB=∠ABC=∠DFB=∠ADF=90°,∠AFB=∠AFD=45°.
在△PFB和△PFD中
,
∴△PFB≌△PFD(SAS),
∴PD=PB,∠1=∠2.
∵DP⊥PC,
∴∠CPD=∠CPH=90°
∴∠3+∠4=90°.
∵∠2+∠4=90°,
∴∠2=∠3,
∴∠1=∠3,
∴PC=PB=PD,
∴△PCD为等腰Rt△,且CD=3
,由勾股定理,得
DP2+CP2=CD2=3.
2DP2=18,
DP=3.
答:DP=3;
(2)如图,连接DE,
在Rt△EBC中,∠5+∠3=90°,∠ABC=∠6+∠1=90°,且∠1=∠3,
∴∠5=∠6,
∴PE=PB=PC=PD.
∵DP⊥CE,
∴DP垂直平分EC,
∴DE=DC.
在Rt△AED和Rt△FCD中
,
∴Rt△AED≌Rt△FCD(HL),
∴AE=CF.
∵BC=BF+CF,
∴BC=AD+AE.
∵AD∥BC,
∴∠DAC+∠ABC=180°.
∵∠ABC=90°,
∴∠DAB=90°.
∵DF⊥BC,
∴∠DFB=∠DFC=90°
∴∠DAB=∠ABC=∠DFB=90°,
∴四边形ABFD是矩形.
∵AD=AB,
∴矩形ABFD是正方形,
∴AB=BF=DF=AD,∠
∴∠DF⊥BC,AD=AB,∠DAB=∠ABC=∠DFB=∠ADF=90°,∠AFB=∠AFD=45°.
在△PFB和△PFD中
|
∴△PFB≌△PFD(SAS),

∴PD=PB,∠1=∠2.
∵DP⊥PC,
∴∠CPD=∠CPH=90°
∴∠3+∠4=90°.
∵∠2+∠4=90°,
∴∠2=∠3,
∴∠1=∠3,
∴PC=PB=PD,
∴△PCD为等腰Rt△,且CD=3
| 2 |
DP2+CP2=CD2=3.
2DP2=18,
DP=3.
答:DP=3;
(2)如图,连接DE,
在Rt△EBC中,∠5+∠3=90°,∠ABC=∠6+∠1=90°,且∠1=∠3,
∴∠5=∠6,
∴PE=PB=PC=PD.
∵DP⊥CE,
∴DP垂直平分EC,
∴DE=DC.
在Rt△AED和Rt△FCD中
|
∴Rt△AED≌Rt△FCD(HL),
∴AE=CF.
∵BC=BF+CF,
∴BC=AD+AE.
点评:本题考查了正方形的判定与性质的运用,全等三角形的判定与性质的运用,直角三角形的性质的运用,中垂线的判定与性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列条件中,不能判定三角形全等的是( )
| A、三条边对应相等 |
| B、两边和其中一边对角对应相等 |
| C、两边和夹角对应相等 |
| D、两角和一边对应相等 |
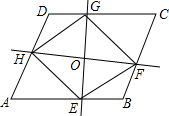 如图,过?ABCD的对角线AC的中点O作互相垂直的两条直线,两直线分别与AB、BC、CD、DA相交于E、F、G、H四点,依次连接EF、FG、GH、HE,试判断四边形EFGH的形状,并说明理由.
如图,过?ABCD的对角线AC的中点O作互相垂直的两条直线,两直线分别与AB、BC、CD、DA相交于E、F、G、H四点,依次连接EF、FG、GH、HE,试判断四边形EFGH的形状,并说明理由. 如图,O为线段AB的中点,分别过点A,B作AB的垂线,与过点O的直线相交于点C,D,求证:O点是CD的中点.
如图,O为线段AB的中点,分别过点A,B作AB的垂线,与过点O的直线相交于点C,D,求证:O点是CD的中点.
 已知:正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF.画出∠EDF,猜想∠EDF的度数并写出计算过程.
已知:正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,BF=2AF.画出∠EDF,猜想∠EDF的度数并写出计算过程.