题目内容
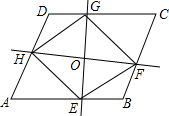 如图,过?ABCD的对角线AC的中点O作互相垂直的两条直线,两直线分别与AB、BC、CD、DA相交于E、F、G、H四点,依次连接EF、FG、GH、HE,试判断四边形EFGH的形状,并说明理由.
如图,过?ABCD的对角线AC的中点O作互相垂直的两条直线,两直线分别与AB、BC、CD、DA相交于E、F、G、H四点,依次连接EF、FG、GH、HE,试判断四边形EFGH的形状,并说明理由.考点:菱形的判定,全等三角形的判定与性质,平行四边形的性质
专题:
分析:根据平行四边形的对角线互相平分可得OA=OC,再根据两直线平行,内错角相等可得∠OAE=∠OCG,然后利用“角边角”证明△AOE和△COG全等,根据全等三角形对应边相等可得OE=OG,同理可得OF=OH,再根据对角线互相平分的四边形是平行四边形判断出四边形EFGH是平行四边形,然后根据对角线互相垂直的平行四边形是菱形解答.
解答:解:四边形EFGH是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAO=∠GCO,
在△EAO和△CGO中,
,
∴△EAO≌△CGO(ASA),
∴OE=OG,
同理可得OH=OF
又∵HF⊥EG,
∴四边形EFGH是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAO=∠GCO,
在△EAO和△CGO中,
|
∴△EAO≌△CGO(ASA),
∴OE=OG,
同理可得OH=OF
又∵HF⊥EG,
∴四边形EFGH是菱形.
点评:本题考查了平行四边形的性质,菱形的判定,熟记性质并求出三角形全等从而得到对角线被互相平分是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
若单项式-3a2mb与a2b3-n是同类项,则m+n=( )
| A、2 | B、3 | C、4 | D、5 |
在-2,1,0,-4中,最小的数是( )
| A、-4 | B、0 | C、1 | D、-2 |
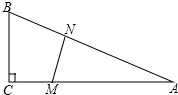 如图,在△ABC中,∠C=90°,BC=5m,AC=12m.M点在线段CA上,从C向A运动,速度为1m/s;同时N点在线段AB上,从A向B运动,速度为2m/s.运动时间为t s.
如图,在△ABC中,∠C=90°,BC=5m,AC=12m.M点在线段CA上,从C向A运动,速度为1m/s;同时N点在线段AB上,从A向B运动,速度为2m/s.运动时间为t s. 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E.