题目内容
 如图,O为线段AB的中点,分别过点A,B作AB的垂线,与过点O的直线相交于点C,D,求证:O点是CD的中点.
如图,O为线段AB的中点,分别过点A,B作AB的垂线,与过点O的直线相交于点C,D,求证:O点是CD的中点.考点:全等三角形的判定与性质
专题:证明题
分析:由CA⊥AB,DB⊥AB就可以得出∠A=∠B=90°,AC∥BD,就有∠C=∠D,就可以得出△AOC≌△BOD,进而得出结论.
解答:证明:∵CA⊥AB,DB⊥AB,
∴∠A=∠B=90°,AC∥BD,
∴∠C=∠D.
∵O为线段AB的中点,
∴AO=BO.
在△AOC和△BOD中,
,
∴△AOC≌△BOD(AAS),
∴CO=DO,
∴O点是CD的中点.
∴∠A=∠B=90°,AC∥BD,
∴∠C=∠D.
∵O为线段AB的中点,
∴AO=BO.
在△AOC和△BOD中,
|
∴△AOC≌△BOD(AAS),
∴CO=DO,
∴O点是CD的中点.
点评:本题考查了垂直的性质的运用,平行线的判定及性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若x是0.25的平方根,则x的值是( )
| A、0.5 | B、-0.5 |
| C、0.05 | D、±0.5 |
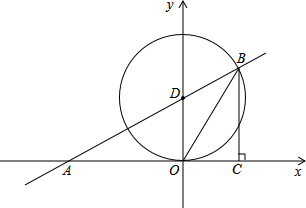
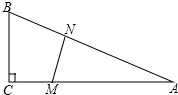 如图,在△ABC中,∠C=90°,BC=5m,AC=12m.M点在线段CA上,从C向A运动,速度为1m/s;同时N点在线段AB上,从A向B运动,速度为2m/s.运动时间为t s.
如图,在△ABC中,∠C=90°,BC=5m,AC=12m.M点在线段CA上,从C向A运动,速度为1m/s;同时N点在线段AB上,从A向B运动,速度为2m/s.运动时间为t s.
 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E.
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB,DF⊥BC于F,连接AF,P为AF上一点,连接DP、CP,且DP⊥CP,CP交DF于G,CP的延长线交AB于E. 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点. 己知y-3与x成正比例,当x=-1时,y=0.
己知y-3与x成正比例,当x=-1时,y=0.