题目内容
17.一个直角三角形三边的长是三个连续的整数,求这个三角形三边的长及这个三角形的周长L和面积S.分析 设三个连续的整数分别为x-1、x、x+1(x>1),由勾股定理可得出关于x的一元二次方程解之即可得出x的值,由此即可得出该三角形的三边长,再根据三角形的周长及面积公式即可求出L、S的值.
解答 解:设三个连续的整数分别为x-1、x、x+1(x>1),
由勾股定理得:(x-1)2+x2=(x+1)2,
解得:x=4或x=0(舍去),
∴这个三角形三边的长度为3、4、5.
∴三角形的周长L=3+4+5=12,三角形的面积S=$\frac{1}{2}$×3×4=6.
点评 本题考查了一元二次方程的应用、勾股定理以及三角的周长与面积,根据勾股定理列出关于x的一元二次方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.如果不等式组$\left\{\begin{array}{l}{-1<x≤3}\\{x>m}\end{array}\right.$ 有解,那么m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<-1 | D. | -1<m<3 |
2.△ABC中,AB=13,BC=10,BC边上中线AP=12,则AB,AC关系为( )
| A. | AB>AC | B. | AB=AC | C. | AB<AC | D. | 无法确定 |
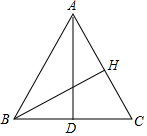 如图,AD是△ABC的中线,AD=12,AB=13,BC=10,
如图,AD是△ABC的中线,AD=12,AB=13,BC=10, 如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.
如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.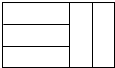 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.