题目内容
12. 如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.
如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.
分析 根据勾股定理求得AC的长,再在三角形ACD中可知三边关系为:DC2=AC2+AD2,可得三角形ACD为直角三角形,然后两三角形的面积和就是所求四边形的面积.
解答 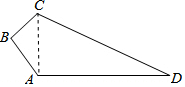 解:连接AC,
解:连接AC,
∵AB=4,BC=3,AD=12,DC=13,∠B=90°,
∴在直角三角形ABC中有:BC2+AB2=AC2,即AC2=9+16=25,
∴AC=5,
又∵AD2=144,DC2=169,
∴AC2+AD2=144+25=169=DC2,即DC2=AC2+AD2,
∴三角形ACD是直角三角形,∠CAD=90°,
∴S四边形ABCD=S△ABC+S△CAD=$\frac{1}{2}$×BC×BA+$\frac{1}{2}$×AC×AD=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=6+30=36.
点评 此题考查了勾股定理,以及勾股定理的逆定理,三角形的面积公式,熟练掌握勾股定理及勾股定理的逆定理是解本题的关键.

练习册系列答案
相关题目
20.算式[(-8)-□]÷(-2)=4中,□表示的数是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
4.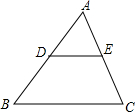 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
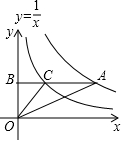 如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.
如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.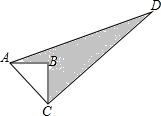 如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.