题目内容
8.已知实数a,b,c满足:|a-b|=5,|b-c|=7,则|a-c|=2或12.分析 根据绝对值性质得出a-b=5或a-b=-5,b-c=7或b-c=-7,从而罗列出所有情况:$\left\{\begin{array}{l}{a-b=5}\\{b-c=7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=5}\\{b-c=-7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=-5}\\{b-c=7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=-5}\\{b-c=-7}\end{array}\right.$,上下两式相加可得a-c,进而得出答案.
解答 解:∵|a-b|=5,|b-c|=7,
∴a-b=5或a-b=-5,b-c=7或b-c=-7,
则$\left\{\begin{array}{l}{a-b=5}\\{b-c=7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=5}\\{b-c=-7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=-5}\\{b-c=7}\end{array}\right.$或$\left\{\begin{array}{l}{a-b=-5}\\{b-c=-7}\end{array}\right.$,
上下两式相加可得a-c=12或a-c=-2或a-c=2或a-c=-12,
即|a-c|=2或12,
故答案为:2或12.
点评 本题主要考查绝对值,熟练掌握①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零是解题的关键.

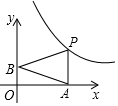 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )| A. | 越来越小 | B. | 越来越大 | C. | 不变 | D. | 先变大后变小 |
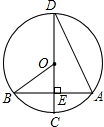 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
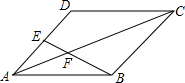 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.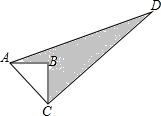 如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.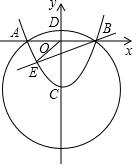 如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D.
如图,抛物线y=ax2-4与x轴相交于A(-3,0)、B,与y轴相交于点C.以点C为圆心,CA长为半径画⊙C,⊙C与y轴的正半轴相交于点D.