题目内容
5.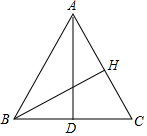 如图,AD是△ABC的中线,AD=12,AB=13,BC=10,
如图,AD是△ABC的中线,AD=12,AB=13,BC=10,(1)求AC的长;
(2)若AC边上的高为BH,求出BH的长.
分析 (1)首先利用勾股定理逆定理证明∠ADB=90°,再利用勾股定理计算出AC的长即可;
(2)根据三角形的面积公式代入数计算即可求出BH的长.
解答 解:(1)∵AD是BC的中线,BC=10,
∴BD=CD=5,
∵122+52=132,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=13;
(2)$\frac{1}{2}$×10×12=60,
60×2÷13=$\frac{120}{13}$.
答:BH的长是$\frac{120}{13}$.
点评 此题主要考查了勾股定理,以及勾股定理逆定理,根据题意证明∠ADC=90°是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.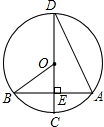 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
20.算式[(-8)-□]÷(-2)=4中,□表示的数是( )
| A. | 1 | B. | -1 | C. | -2 | D. | 0 |
14.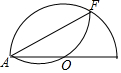 将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
 将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )
将一个半径为5的半圆O,如图折叠,使弧AF经过点O,则折痕AF的长度为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
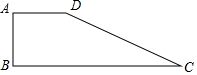 如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.
如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.