题目内容
9.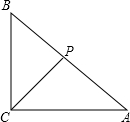 已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.
已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.(1)如果PD∥BC,求证:AC•CD=AD•BC;
(2)如果∠BPD=135°,求证:CP2=CB•CD.
分析 (1)根据角平分线的性质和平行线的性质证得∠CPD=∠PCA,得出PD=CD,然后证得△APD∽△ABC,根据相似三角形的性质即可证得结论;
(2)根据三角形内角和定理求得∠B=∠CPD,即可证得△PCB∽△PDC根据相似三角形的性质即可证得结论.
解答 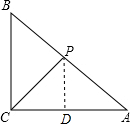 (1)证明:如图,∵PD∥BC,
(1)证明:如图,∵PD∥BC,
∴∠PCB=∠CPD,
∵∠PCB=∠PCA,
∴∠CPD=∠PCA,
∴PD=CD,
∵PD∥BC,
∴△APD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{PD}{BC}$,
∴AC•PD=AD•BC,
∴AC•CD=AD•BC;
(2)证明:∵Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,
∴∠PCB=∠PCA=45°,
∵∠B+45°+∠CPB=180°,
∴∠B+∠CPB=135°,
∵∠BPD=135°,
∴∠CPB+∠CPD=135°,
∴∠B=∠CPD,
∴△PCB∽△PDC,
∴$\frac{CB}{CP}$=$\frac{CP}{CD}$,
∴CP2=CB•CD.
点评 本题考查了三角形相似的判定和性质,熟练掌握相似三角形的判定方法是解题的关键.

练习册系列答案
相关题目
20.已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=$\frac{-{m}^{2}-1}{x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
17.下列不等式变形正确的是( )
| A. | 由a>b得-2a>-2b | B. | 由-1>-2得$\frac{1}{\sqrt{2}}$>$\frac{2}{\sqrt{2}}$ | C. | 由a>b得ac>bc | D. | 由a>b得-a<-b |
14.如图所示的几何体的左视图是( )


| A. |  | B. |  | C. |  | D. |  |
 在平面直角坐标系中,已知点A(-2,1),B(-1,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的△A1B1C1.
在平面直角坐标系中,已知点A(-2,1),B(-1,0),C(0,1),请在图中画出△ABC,并画出与△ABC关于原点O对称的△A1B1C1.